
【题目】近年电子商务蓬勃发展,现从某电子商务平台评价系统中随机选出200次成功交易,并对其评价进行统计,统计结果显示:网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答在犯错误的概率不超过0.10的前提下,能否认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(2)为进一步提高购物者的满意度,平台按分层抽样方法从200次交易中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附: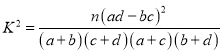 (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)![]() 列联表答案见解析,网购者对商品满意与对快递满意之间有关系.(2)
列联表答案见解析,网购者对商品满意与对快递满意之间有关系.(2)![]()
【解析】
(1)由题意完成![]() 列联表,将数据代入
列联表,将数据代入![]() 中,并与2.706比较大小,即可得到结果;
中,并与2.706比较大小,即可得到结果;
(2)由分层抽样求得10次中对商品和快递都满意的交易有4次,进而求解即可.
(1)由题,对商品满意的交易有![]() 次;对快递满意的有
次;对快递满意的有![]() 次,
次,
则![]() 列联表:
列联表:
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
所以![]()
![]() ,
,
由于![]() ,所以根据以上数据,在犯错误的概率不超过
,所以根据以上数据,在犯错误的概率不超过![]() 的前提下没有证据表明“网购者对商品满意与对快递满意之间有关系”.
的前提下没有证据表明“网购者对商品满意与对快递满意之间有关系”.
(2)由(1)中的![]() 列联表,
列联表,
抽取的![]() 次交易中,对商品和快递都满意的交易有
次交易中,对商品和快递都满意的交易有![]() 次,
次,
所以在抽取的![]() 次交易中,至少一次对商品和快递都满意的概率是
次交易中,至少一次对商品和快递都满意的概率是![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,
,![]() 点又恰为抛物线
点又恰为抛物线![]() 的焦点,以
的焦点,以![]() 为直径的圆与椭圆
为直径的圆与椭圆![]() 仅有两个公共点.
仅有两个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,记点
两点,记点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,![]() .直线
.直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,记
两点,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() .
.
(ⅰ)证明:![]() 的周长为定值;
的周长为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准![]() ,用电量不超过
,用电量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示,用电量在
分组的频率分布直方图如图所示,用电量在![]() 的居民户数比用电量在
的居民户数比用电量在![]() 的居民户数多11户.
的居民户数多11户.
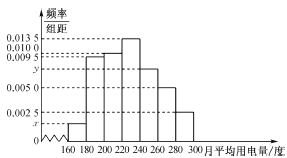
(1)求直方图中![]() ,
,![]() 的值;
的值;
(2)(i)用样本估计总体,如果希望至少85%的居民月用电量低于标准,求月用电量的最低标准应定为多少度,并说明理由;
(ii)若将频率视为概率,现从该市所有居民中随机抽取3户,其中月用电量低于(i)中最低标准的居民户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的两顶点坐标
的两顶点坐标![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的内切圆,在边
的内切圆,在边![]() ,
,![]() ,
,![]() 上的切点分别为
上的切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
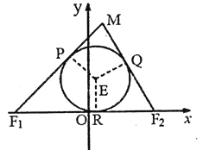
(Ⅰ)求证:![]() 为定值,并求出动点
为定值,并求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过![]() 的斜率不为零直线交曲线
的斜率不为零直线交曲线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为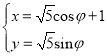 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() (任意项都不为零)的前
(任意项都不为零)的前![]() 项和为
项和为![]() ,首项为
,首项为![]() ,对于任意
,对于任意![]() ,满足
,满足![]() .
.
(1)数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() 使得
使得![]() 成等比数列,且
成等比数列,且![]() 成等差数列?若存在,试求
成等差数列?若存在,试求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() ,
, ,若由
,若由![]() 的前
的前![]() 项依次构成的数列是单调递增数列,求正整数
项依次构成的数列是单调递增数列,求正整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个数列![]() 、
、![]() ,当
,当![]() 和
和![]() 同时在
同时在![]() 时取得相同的最大值,我们称
时取得相同的最大值,我们称![]() 与
与![]() 具有性质
具有性质![]() ,其中
,其中![]() .
.
(1)设![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() (
(![]() ),
),![]() ,记
,记![]() ,
,![]() ,
,![]() ,依次下去,
,依次下去,![]() ,组成的数列是
,组成的数列是![]() ;同样地,
;同样地,![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() (
(![]() ),
),![]() ,记
,记![]() ,
,![]() ,
,![]() ,依次下去,
,依次下去,![]() ,组成的数列是
,组成的数列是![]() ;判别
;判别![]() 与
与![]() 是否具有性质
是否具有性质![]() ,请说明理由;
,请说明理由;
(2)数列![]() 的前
的前![]() 项和是
项和是![]() ,数列
,数列![]() 的前
的前![]() 项和是
项和是![]() ,若
,若![]() 与
与![]() 具有性质
具有性质![]() ,
,![]() ,则这样的数列
,则这样的数列![]() 一共有多少个?请说明理由;
一共有多少个?请说明理由;
(3)两个有限项数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 具有性质
具有性质![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com