
(1)m为何值时,f(x)=x2+2mx+3m+4.
①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
解析 (1)①f(x)=x2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根
⇔Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②法一 设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
由题意,在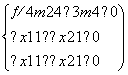 ⇔
⇔
 ⇔
⇔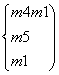
∴-5<m<-1.故m的取值范围为(-5,-1).
法二 由题意,知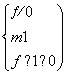 即
即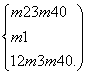
∴-5<m<-1.∴m的取值范围为(-5,-1).
(2)令f(x)=0,得|4x-x2|+a=0,
即|4x-x2|=-a.
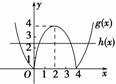
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,即-4<a<0时,g(x)与h(x)的图象有4个交点,即f(x)有4个零点.故a的取值范围为(-4,0).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
若函数f(x)=x2+mx+1有两个不同的零点,则实数m的取值范围是 ( )
A.(-1,1) B.(-2,2)
C.(-∞,-2)∪(2,+∞) D.(-∞,-1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________ km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com