练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
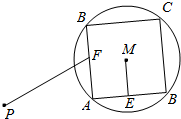
    11．如图，已知圆M的半径为2，点P与圆心M的距离为4，正方形ABCD是圆M的内接四边形，E，F是边AB，AD的中点，当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是（　　）
    A．[-2，2]B．[-2$\sqrt{2}$，2$\sqrt{2}$]C．[-4，4]D．[-4$\sqrt{2}$，4$\sqrt{2}$]

    分析 由条件利用两个向量的加减法的法则，以及其几何意义，以及余弦函数的值域求得$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围．

    解答 解：$\overrightarrow{PF}$•$\overrightarrow{ME}$=（$\overrightarrow{PM}$+$\overrightarrow{MF}$）•$\overrightarrow{ME}$=$\overrightarrow{PM}$•$\overrightarrow{ME}$+$\overrightarrow{MF}•\overrightarrow{ME}$=$\overrightarrow{PM}$•$\overrightarrow{ME}$=4$\sqrt{2}$•cosθ （θ 是$\overrightarrow{PM}$、$\overrightarrow{ME}$的夹角）．
    故当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是[-4$\sqrt{2}$，4$\sqrt{2}$]，
    故选：D．

    点评 本题主要考查两个向量的加减法的法则，以及其几何意义，余弦函数的值域，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．在△ABC中，记角A，B，C的对边为a，b，c，角A为锐角，设向量$\overrightarrow m$=（cosA，sinA），$\overrightarrow n$=（cosA，-sinA），且$\overrightarrow m$•$\overrightarrow n$=$\frac{1}{2}$
    （I）求角A的大小及向量$\overrightarrow m$与$\overrightarrow n$的夹角；
    （II）若a=$\sqrt{5}$，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在△ABC中，A=60°，b=3，面积S=3$\sqrt{3}$，则a=$\sqrt{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．小明家住C区，他的学校在D区，从家骑自行车到学校的路有L1、L2．两条路线（如图），路线L1上有A1、A2、A3三个路口，各路口遇到红灯的概率均为$\frac{2}{3}$；L2路线上有B1、B2两个路口，各路口遇到红灯的概率依次为$\frac{3}{4}$、$\frac{3}{5}$．         
    （I）若走L1，路线，求至少遇到1次红灯的概率；
    （Ⅱ）若走L2路线，求遇到红灯次数X的数学期
    （Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助小明从上述两条路线中选择一条最好的上学路线，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知点（1，$\frac{1}{3}$）是函数f（x）=ax（a＞0且a≠1）的图象上一点，等比数列{an}的前n项和为f（n）-c，数列{bn}（bn＞0）的首项为c，且前n项和Sn满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$（n≥2）．
    （1）求数列{an}和{bn}的通项公式；
    （2）若数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}前n项和为Tn，则满足Tn＞$\frac{1000}{2015}$的最小正整数n是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知条件p：函数f（x）=log${\;}_{10-{a}^{2}}$x在（0，+∞）上单调递增；条件q：对于任意实数x．不等式x2-3ax+2a2-$\frac{1}{2}$+a＞0恒成立．如果“p且q”为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=$\frac{2x+3}{3x}$，数列{an}满足a1=1，an+1=f（$\frac{1}{{a}_{n}}$），（n∈N*），
    （1）求数列{an}的通项公式；
    （2）设bn=$\frac{1}{{a}_{n-1}{a}_{n}}$（n≥2），b1=3，求{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．一袋中装有6个形状大小完全相同的小球，分别标有数字1，2，3，其中编号为3的小球有1个，已知从中一次抽取两球，至少抽到1个编号为1的小球的概率为$\frac{4}{5}$．
    （1）求编号为1的小球个数；
    （2）若有放回的抽取3次，每次随机抽取3球，求恰有2次抽到编号为3的小球的概率；
    （3）从袋中随机抽取3个小球，记球的最大编号为X，求随机变量X的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知复数z满足：z（1-i）=2+4i，其中i为虚数单位，则复数z的模为$\sqrt{10}$．

    查看答案和解析>>

    同步练习册答案