
 С����סC��������ѧУ��D�����Ӽ������г���ѧУ��·��L1��L2������·�ߣ���ͼ����·��L1����A1��A2��A3����·�ڣ���·��������Ƶĸ��ʾ�Ϊ$\frac{2}{3}$��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ$\frac{3}{4}$��$\frac{3}{5}$��
С����סC��������ѧУ��D�����Ӽ������г���ѧУ��·��L1��L2������·�ߣ���ͼ����·��L1����A1��A2��A3����·�ڣ���·��������Ƶĸ��ʾ�Ϊ$\frac{2}{3}$��L2·������B1��B2����·�ڣ���·��������Ƶĸ�������Ϊ$\frac{3}{4}$��$\frac{3}{5}$�� ���� ��I���衰��������1�κ�ơ�Ϊ�¼�A��������¼���û��������ƣ����ö���ֲ����ɵó���
��������������¼��ĸ��ʼ��㹫ʽ����ɢ������������������㹫ʽ���ɵó���
����������·��L1ʱ���Ӷ���ֲ����ɵó��������Ƚ�������·����ѧ�����Ĵ�С���ɵó�Ҫѡ���·�ߣ�
��� �⣺��I���衰��������1�κ�ơ�Ϊ�¼�A��������¼���û��������ƣ�
��P��A��=1-${C}_{3}^{0}����\frac{1}{2}��^{3}$=$\frac{7}{8}$��
������L1·�ߣ���������1�κ�Ƶĸ���Ϊ$\frac{7}{8}$��
���������⣬X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=��1-$\frac{3}{4}$������1-$\frac{3}{5}$��=$\frac{1}{10}$��P��X=1��=$\frac{3}{4}$����1-$\frac{3}{5}$��+��1-$\frac{3}{4}$����$\frac{3}{5}$=$\frac{9}{20}$��
P��X=2��=$\frac{3}{4}$��$\frac{3}{5}$=$\frac{9}{20}$��
�������X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{9}{20}$ | $\frac{9}{20}$ |
���� �������ն���ֲ��С�������¼��ĸ��ʼ��㹫ʽ����ɢ������������������㹫ʽ���������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڢ� | B�� | �ڢ� | C�� | �ۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 5 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��ֱ�Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
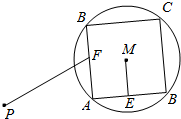 ��ͼ����֪ԲM�İ뾶Ϊ2����P��Բ��M�ľ���Ϊ4��������ABCD��ԲM���ڽ��ı��Σ�E��F�DZ�AB��AD���е㣬��������ABCD��Բ��Mת��ʱ��$\overrightarrow{PF}$•$\overrightarrow{ME}$��ȡֵ��Χ�ǣ�������
��ͼ����֪ԲM�İ뾶Ϊ2����P��Բ��M�ľ���Ϊ4��������ABCD��ԲM���ڽ��ı��Σ�E��F�DZ�AB��AD���е㣬��������ABCD��Բ��Mת��ʱ��$\overrightarrow{PF}$•$\overrightarrow{ME}$��ȡֵ��Χ�ǣ�������| A�� | [-2��2] | B�� | [-2$\sqrt{2}$��2$\sqrt{2}$] | C�� | [-4��4] | D�� | [-4$\sqrt{2}$��4$\sqrt{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -12 | B�� | -6 | C�� | 6 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com