
分析 根据对数函数的单调性便有10-a2>1,从而可得出-3<a<3,而由不等式${x}^{2}-3ax+2{a}^{2}-\frac{1}{2}+a>0$恒成立,便可得到△<0,这样可解出$2-\sqrt{2}<a<2+\sqrt{2}$,然后根据p且q为真命题,便得到p真q真,从而解不等式组$\left\{\begin{array}{l}{-3<a<3}\\{2-\sqrt{2}<a<2+\sqrt{2}}\end{array}\right.$即可得出实数a的取值范围.
解答 解:f(x)在(0,+∞)上单调递增;
∴10-a2>1;
∴a2<9;
∴-3<a<3;
不等式${x}^{2}-3ax+2{a}^{2}-\frac{1}{2}+a>0$恒成立;
∴$△=9{a}^{2}-4(2{a}^{2}-\frac{1}{2}+a)={a}^{2}-4a+2<0$;
解得$2-\sqrt{2}<a<2+\sqrt{2}$;
条件p:-3<a<3,条件q:$2-\sqrt{2}<a<2+\sqrt{2}$;
∵p且q为真命题;
∴p,q都为真命题;
∴$\left\{\begin{array}{l}{-3<a<3}\\{2-\sqrt{2}<a<2+\sqrt{2}}\end{array}\right.$;
∴$2-\sqrt{2}<a<3$;
∴实数a的取值范围为$(2-\sqrt{2},3)$.
点评 考查对数函数的单调性,解一元二次不等式,一元二次不等式ax2+bx+c>0的解集为R时,判别式△的取值情况,以及p且q真假和p,q真假的关系.


科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
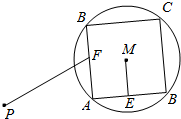 如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )
如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )| A. | [-2,2] | B. | [-2$\sqrt{2}$,2$\sqrt{2}$] | C. | [-4,4] | D. | [-4$\sqrt{2}$,4$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -6 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com