Question

5．已知△ABC的面积为2，E，F是AB，AC的中点，P为直线EF上任意一点，则$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为（　　）

• A． 2
• B． 3
• C． 2$\sqrt{3}$
• D． 4

Answer 1

分析 根据△ABC的面积为2，可得△PBC的面积=1，从而可得PB×PC=$\frac{2}{sin∠BPC}$，故 $\overrightarrow{PC}$•$\overrightarrow{PB}$=PB×PCcos∠BPC=$\frac{2cos∠BPC}{sin∠BPC}$，由余弦定理，有：BC²=BP²+CP²-2BP×CPcos∠BPC，进而可得BC²≥2BP×CP-2BP×CPcos∠BPC．从而 $\overrightarrow{PC}$•$\overrightarrow{PB}$+$\overrightarrow{BC}$²≥$\frac{4-2cos∠BPC}{sin∠BPC}$，利用导数，可得 $\frac{4-2cos∠BPC}{sin∠BPC}$最大值为2$\sqrt{3}$，从可得$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值．

解答 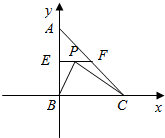解：：∵E、F是AB、AC的中点，∴EF到BC的距离=点A到BC的距离的一半，
∴△ABC的面积=2△PBC的面积，而△ABC的面积=2，∴△PBC的面积=1，
又△PBC的面积=$\frac{1}{2}$PB×PCsin∠BPC，∴PB×PC=$\frac{2}{sin∠BPC}$．
∴$\overrightarrow{PC}$•$\overrightarrow{PB}$=PB×PCcos∠BPC=$\frac{2cos∠BPC}{sin∠BPC}$，
由余弦定理，有：BC²=BP²+CP²-2BP×CPcos∠BPC．
显然，BP、CP都是正数，∴BP²+CP²≥2BP×CP，∴BC²≥2BP×CP-2BP×CPcos∠BPC．
∴$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$≥PB×PCcos∠BPC+2BP×CP-2BP×CPcos∠BPC=$\frac{4-2cos∠BPC}{sin∠BPC}$．
令y=$\frac{4-2cos∠BPC}{sin∠BPC}$，则y′=$\frac{2-4cos∠BPC}{sin2∠BPC}$
令y′=0，则cos∠BPC=$\frac{1}{2}$，此时函数在（0，$\frac{1}{2}$）上单调增，在（ $\frac{1}{2}$，1）上单调减，
∴cos∠BPC=时，$\frac{4-2cos∠BPC}{sin∠BPC}$取得最大值为2$\sqrt{3}$．
∴$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为2$\sqrt{3}$．
故选：C．

点评 本题考查了向量坐标运算、向量共线定理、数量积运算性质、余弦定理、基本不等式的性质、导数的应用，考查了推理能力与计算能力，属于难题．