已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
(1) 
+
=1 (2) -
或
【解析】
解:(1)设M到直线l的距离为d,
根据题意,d=2|MN|.
由此得|4-x|=2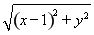
,
化简得+=1,
所以,动点M的轨迹方程为+=1.
(2)法一 由题意,设直线m的方程为y=kx+3,A(x1,y1),B(x2,y2).
将y=kx+3代入+=1中,
有(3+4k2)x2+24kx+24=0,
其中,Δ=(24k)2-4×24(3+4k2)=96(2k2-3)>0,
由求根公式得,
x1+x2=-
, ①
x1x2=
. ②
又因A是PB的中点,
故x2=2x1,③
将③代入①,②,得
x1=-
,
=
,
可得
=,
且k2>,
解得k=-或k=,
所以,直线m的斜率为-或.
法二 由题意,设直线m的方程为y=kx+3,
A(x1,y1),B(x2,y2).
∵A是PB的中点,
∴x1=
,①
y1=
.②
又
+
=1,③
+
=1.④
联立①,②,③,④解得
或
即点B的坐标为(2,0)或(-2,0),
所以,直线m的斜率为-或.
科目：高中数学 来源： 题型：
已知动点M(x,y)到直线l:x = 4的距离是它到点N(1,0)的距离的2倍.
(Ⅰ) 求动点M的轨迹C的方程;
(Ⅱ) 过点P(0,3)的直线m与轨迹C交于A, B两点. 若A是PB的中点, 求直线m的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
,0)的距离与它到y轴距离之差为
.(1)求M点的轨迹E;
(2)M点在E上何处时,|MA|+|MF|的值最小?其中A为(3,2).
查看答案和解析>>
科目：高中数学 来源： 题型：
.(1)求αf(α)+βf(β)的值;
(2)判断f(x)在区间(α,β)上的单调性,并加以证明;
(3)若λ、μ为正实数,证明不等式:|f(
)-f(
)|＜|α-β|.
(文)如图,在平面直角坐标系中,已知动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且
=4.
(1)求动点P的轨迹W的方程;
(2)若点Q的坐标为(2,0),A、B为W上的两个动点,且满足QA⊥QB,点Q到直线AB的距离为d,求d的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋
＝8，则动点M的轨迹是________．