
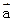 ·
·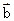 ,其中
,其中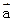 =(m,cos2x),
=(m,cos2x),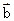 =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(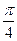 ,2).
,2). 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R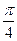 )=m(1+sin
)=m(1+sin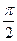 )+cos
)+cos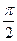 =2,解得m=1.……6分
=2,解得m=1.……6分 x)=1+sin2x+cos2x=1+
x)=1+sin2x+cos2x=1+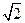 sin(2x+
sin(2x+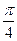 ).
).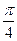 )=-1时,f(x)的最小值为1-
)=-1时,f(x)的最小值为1-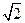 . ……………11分
. ……………11分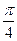 )=-1,得x值的集合为{x|x=k
)=-1,得x值的集合为{x|x=k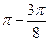 ,k∈Z}.……14分
,k∈Z}.……14分 (x)=ex-e.
(x)=ex-e.  (x)>0得x>1,
(x)>0得x>1, (x)<0得x<1,
(x)<0得x<1, f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立. 由f
f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立. 由f (x)=ex-k=0得x="lnk."
(x)=ex-k=0得x="lnk."  时,f
时,f (x)=ex-k>1-k≥0(x>0). 此时f(x)在[0,+∞
(x)=ex-k>1-k≥0(x>0). 此时f(x)在[0,+∞ 上单调递增. 故f(x)≥f(0)=1>0,符合题意.所以0<k≤1. …………10分②当k∈(1,+∞)时,lnk>0. 当x变化时f
上单调递增. 故f(x)≥f(0)=1>0,符合题意.所以0<k≤1. …………10分②当k∈(1,+∞)时,lnk>0. 当x变化时f (x),f(x)的变化情况如下
(x),f(x)的变化情况如下 :
:| x | (0,lnk) | lnk | (lnk,+∞) |
f (x) (x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
 上,f(x)≥f(lnk)=k-klnk.
上,f(x)≥f(lnk)=k-klnk.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源:不详 题型:解答题
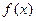 ,(
,(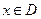 ),若同时满足以下条件:
),若同时满足以下条件: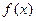 在D上单调递减或单调递增
在D上单调递减或单调递增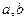 ]
]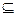 D,使
D,使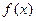 在[
在[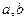 ]上的值域是[
]上的值域是[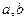 ],那么称
],那么称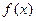 (
(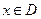 )为闭函数。
)为闭函数。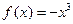 符合条件②的区间[
符合条件②的区间[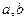 ];
];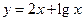 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[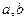 ];若不是请说明理由;
];若不是请说明理由;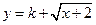 是闭函数,求实数
是闭函数,求实数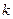 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com