
如图,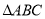 在平面
在平面 内,
内,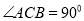 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面 外一个动点,且PC=
外一个动点,且PC= ,
,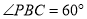

(1)问当PA的长为多少时,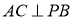
(2)当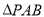 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
(1)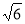 ;(2)
;(2)
【解析】
试题分析:(1)由分析可知当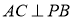 时,
时,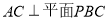 ,则
,则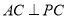 ,由勾股定理可求得
,由勾股定理可求得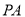 。(2)因为
。(2)因为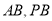 为定值,且
为定值,且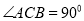 ,
,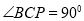 ,所以当
,所以当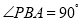 时,
时,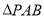 的面积取得最大值。分析可知
的面积取得最大值。分析可知 均是以
均是以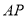 为底的等腰三角形,故取
为底的等腰三角形,故取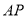 中点
中点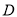 ,连接
,连接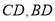 。则有
。则有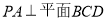 ,从而可得
,从而可得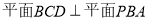 。过
。过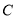 作
作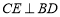 ,E为垂足,从而可得
,E为垂足,从而可得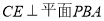 ,所以
,所以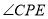 就是直线
就是直线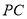 与平面
与平面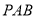 所成角,在
所成角,在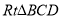 中即可求此角。
中即可求此角。
试题解析:(1)因为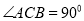 ,所以
,所以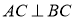 ,当
,当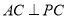 时,
时,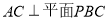 ,而
,而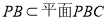 ,所以
,所以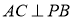 时,此时,
时,此时,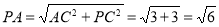 ,即当
,即当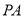 =
=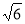 时,
时,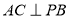
(2)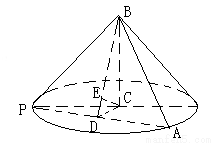
在 中,因为PC=
中,因为PC=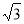 ,
,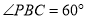 ,
,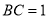 ,所以
,所以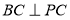 ,
,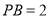 .当
.当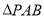 的面积取得最大值时,
的面积取得最大值时,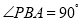 ,(如图)在
,(如图)在 中,因为
中,因为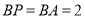 ,取
,取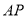 中点
中点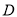 ,连接
,连接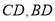 。因为
。因为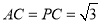 且点
且点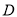 为
为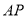 中点,所以
中点,所以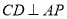 ,因为
,因为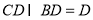 ,所以
,所以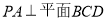 ,由此可求得
,由此可求得 ,又在
,又在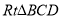 中,
中,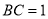 ,所以
,所以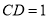 ,过
,过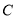 作
作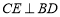 ,E为垂足,由于
,E为垂足,由于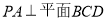 ,所以,
,所以,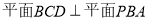 ,由两个平面互相垂直的性质可知:
,由两个平面互相垂直的性质可知: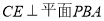 ,所以
,所以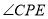 就是直线
就是直线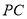 与平面
与平面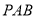 所成角,在
所成角,在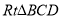 中,可求得
中,可求得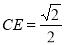 ,在
,在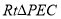 中,
中,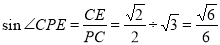 ,所以直线
,所以直线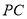 与平面
与平面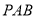 所成角的正弦值是
所成角的正弦值是 .
.
考点:1线线垂直、线面垂直;2线面角。


科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
阅读如图所示的程序框图,则输出结果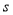 的值为( )
的值为( )

A.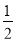 B.
B.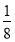 C.
C.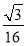 D.
D.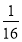
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中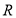 为实数集,
为实数集,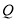 为有理数集,则关于函数
为有理数集,则关于函数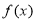 有如下四个命题:
有如下四个命题:
①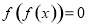 ; ②函数
; ②函数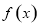 是偶函数;
是偶函数;
③任取一个不为零的有理数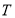 ,
,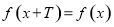 对任意的
对任意的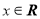 恒成立;
恒成立;
④存在三个点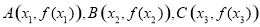 ,使得
,使得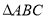 为等边三角形.
为等边三角形.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“都是红球”
C.“至少有一个黑球”与“至少有一个红球”
D.“恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
已知双曲线C的方程是: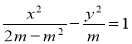 (
(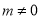 ),若双曲线的离心率
),若双曲线的离心率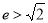 ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A. 1<m<2. B .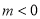 C .
C .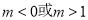 D.
D.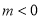 或1<m<2.
或1<m<2.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:填空题
某几何体的三视图(单位:cm)如右图所示,则此几何体的体积等于cm3.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:填空题
已知定义在R上的函数f(x),g(x)满足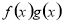 =ax,且f′(x)g(x)+ f(x)·g′(x) <0,
=ax,且f′(x)g(x)+ f(x)·g′(x) <0,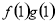 +
+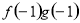 =
=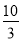 ,若有穷数列{
,若有穷数列{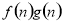 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于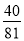 ,则n等于 .
,则n等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com