
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中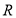 为实数集,
为实数集,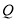 为有理数集,则关于函数
为有理数集,则关于函数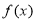 有如下四个命题:
有如下四个命题:
①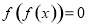 ; ②函数
; ②函数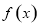 是偶函数;
是偶函数;
③任取一个不为零的有理数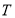 ,
,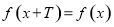 对任意的
对任意的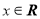 恒成立;
恒成立;
④存在三个点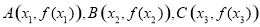 ,使得
,使得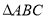 为等边三角形.
为等边三角形.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:填空题
在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为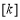 ,即
,即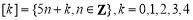 . 给出如下四个结论:
. 给出如下四个结论:
①2011∈[1];②-3∈[3];③Z=[0]∪[1]∪[2]∪[3]∪[4];④“整数a,b属于同一‘类’”的充要条件是“a-b∈[0]”.
其中,正确的结论的个数是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:解答题
已知向量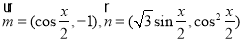 ,设函数
,设函数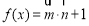
(1)求函数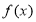 的单调递增区间;
的单调递增区间;
(2)在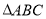 中,角
中,角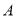 、
、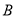 、
、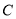 的对边分别为
的对边分别为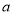 、
、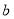 、
、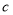 ,且满足
,且满足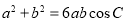 ,
,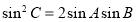 ,求
,求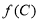 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:解答题
已知函数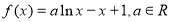 .
.
(1)求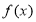 的单调区间;
的单调区间;
(2)若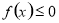 在
在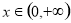 上恒成立,求所有实数
上恒成立,求所有实数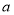 的值;
的值;
(3)对任意的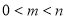 ,证明:
,证明: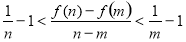
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
莱因德纸草书》是世界上最古老的数学著作之一,书中有这样的一道题目:把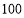 个面包分给
个面包分给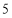 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的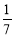 是较小的两份之和,则最小的
是较小的两份之和,则最小的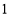 份为( )
份为( )
A.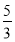 B.
B.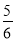 C.
C.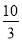 D.
D.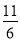
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:解答题
如图,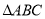 在平面
在平面 内,
内,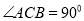 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面 外一个动点,且PC=
外一个动点,且PC= ,
,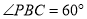

(1)问当PA的长为多少时,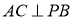
(2)当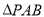 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
设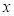 为非零实数,则p:
为非零实数,则p: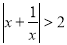 是q:
是q: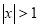 成立的 ( )
成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:选择题
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
A.28 B.47 C.76 D.123
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com