
【题目】已知函数![]() ,
,![]() .
.
![]() 若
若![]() 是函数
是函数![]() 的极值点,求曲线
的极值点,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
![]() 若函数
若函数![]() 在区间
在区间![]() 上为单调递减函数,求实数a的取值范围;
上为单调递减函数,求实数a的取值范围;
![]() 设m,n为正实数,且
设m,n为正实数,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
![]() 求出导函数,得到函数
求出导函数,得到函数![]() 的极值点,解得
的极值点,解得![]() ,求出切线的斜率为
,求出切线的斜率为![]() ,切点为
,切点为![]() ,然后利用点斜式求解切线方程;
,然后利用点斜式求解切线方程;![]() 由
由![]() 知
知![]() ,利用函数
,利用函数![]() 在区间
在区间![]() 上为单调递减函数,得到
上为单调递减函数,得到![]() 在区间
在区间![]() 上恒成立,推出
上恒成立,推出![]() ,设
,设![]() ,
,![]() ,
,![]() ,利用基本不等式
,利用基本不等式![]() ,再求出函数的最大值,可得实数
,再求出函数的最大值,可得实数![]() 的取值范围;
的取值范围;![]() 利用分析法证明,要证
利用分析法证明,要证![]() ,只需证
,只需证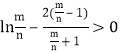 ,设
,设![]() ,
,![]() ,利用导数研究函数的单调性,可得
,利用导数研究函数的单调性,可得![]() ,从而可得结论.
,从而可得结论.
![]() ,
,![]() .
.
![]()
![]() 是函数
是函数![]() 的极值点,
的极值点,![]() ,解得
,解得![]() ,
,
经检验,当![]() 时,
时,![]() 是函数
是函数![]() 的极小值点,符合题意
的极小值点,符合题意![]()
此时切线的斜率为![]() ,切点为
,切点为![]() ,
,
则所求切线的方程为![]()
![]() 由
由![]() 知
知![]()
因为函数![]() 在区间
在区间![]() 上为单调递减函数,
上为单调递减函数,
所以不等式![]() 在区间
在区间![]() 上恒成立
上恒成立![]()
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
当且仅当![]() 时,即
时,即![]() 时,
时,![]() ,
,
又因为函数![]() 在区间
在区间![]() 上为单调递减,在区间
上为单调递减,在区间![]() 上为单调递增,
上为单调递增,
且![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,也即
,也即![]()
则所求实数a的取值范围是![]()
![]() ,n为正实数,且
,n为正实数,且![]() ,
,![]() 要证
要证![]() ,只需证
,只需证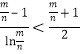
即证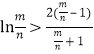 只需证
只需证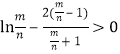
设![]() ,
,![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
即函数![]() 在
在![]() 上是单调递增,
上是单调递增,
又![]() ,
,![]() ,即
,即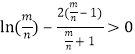 成立,
成立,
也即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
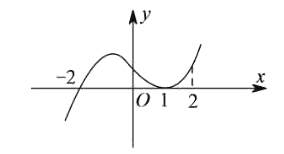
【题目】如图是函数![]() 的导函数
的导函数![]() 的图象,给出下列命题:①-2是函数
的图象,给出下列命题:①-2是函数![]() 的极值点;②1是函数
的极值点;②1是函数![]() 的极值点;③
的极值点;③![]() 在
在![]() 处切线的斜率小于零;④
处切线的斜率小于零;④![]() 在区间
在区间![]() 上单调递增.则正确命题的序号是_______.(写出所有正确命题的序号)
上单调递增.则正确命题的序号是_______.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域和值域均为[-a,a]的函数y=![]() 和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
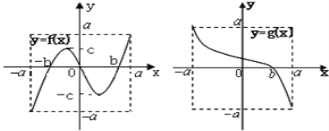
A.方程f[g(x)]=0有且仅有三个解B.方程g[f(x)]=0有且仅有三个解
C.方程f[f(x)]=0有且仅有九个解D.方程g[g(x)]=0有且仅有一个解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,各类手机娱乐软件也如雨后春笋般涌现. 如表中统计的是某手机娱乐软件自2018年8月初推出后至2019年4月底的月新注册用户数,记月份代码为![]() (如
(如![]() 对应于2018年8月份,
对应于2018年8月份,![]() 对应于2018年9月份,…,
对应于2018年9月份,…,![]() 对应于2019年4月份),月新注册用户数为
对应于2019年4月份),月新注册用户数为![]() (单位:百万人)
(单位:百万人)
![]()
(1)请依据上表的统计数据,判断月新注册用户与月份线性相关性的强弱;
(2)求出月新注册用户关于月份的线性回归方程,并预测2019年5月份的新注册用户总数.
参考数据:![]() ,
,![]() ,
,![]() .
.
回归直线的斜率和截距公式: ,
,![]() .
.
相关系数 (当
(当![]() 时,认为两相关变量相关性很强. )
时,认为两相关变量相关性很强. )
注意:两问的计算结果均保留两位小数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com