
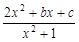 (b<0)的值域是[1,3],
(b<0)的值域是[1,3],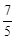 ≤F(|t-
≤F(|t-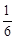 |-|t+
|-|t+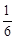 |)≤lg
|)≤lg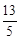 .
. ,则(y-2)x2-bx+y-c="0" ①
,则(y-2)x2-bx+y-c="0" ①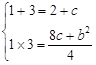 ∴c=2,b=-2,b=2(舍)
∴c=2,b=-2,b=2(舍) >0,
>0,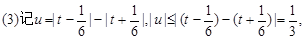
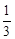 ≤u≤
≤u≤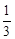 ,根据F(x)的单调性知
,根据F(x)的单调性知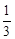 )≤F(u)≤F(
)≤F(u)≤F(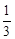 ),∴lg
),∴lg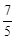 ≤F(|t-
≤F(|t- |-|t+
|-|t+ |)≤lg
|)≤lg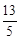 对任意实数t成立.
对任意实数t成立.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
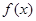 是定义在
是定义在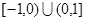 上的偶函数,当
上的偶函数,当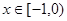 时,
时,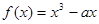 (
(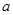 是实数)。
是实数)。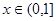 时,求f(x)的解析式;
时,求f(x)的解析式;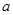 的取值范围;
的取值范围;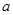 ,使得当
,使得当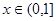 时,f(x)有最大值1.
时,f(x)有最大值1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com