
分析 以OC为对角线,$\overrightarrow{OA}$,$\overrightarrow{OB}$方向为边作?ODCE,由$\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{OE}$,能求出$\frac{λ}{μ}$的值.
解答 解: 以OC为对角线,$\overrightarrow{OA}$,$\overrightarrow{OB}$方向为边作?ODCE,
以OC为对角线,$\overrightarrow{OA}$,$\overrightarrow{OB}$方向为边作?ODCE,
∵平面内三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,
$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=$\frac{3}{2}$,|$\overrightarrow{OC}$|=2$\sqrt{3}$,
∴∠COD=30°,∠COE=∠OCD=90°,
在Rt△OCD中,∵|$\overrightarrow{OC}$|=2$\sqrt{3}$,∴|$\overrightarrow{OD}$|=$\frac{|\overrightarrow{OC}|}{cos30°}$=4,
在Rt△OCE中,|$\overrightarrow{OE}$|=|$\overrightarrow{OC}$|•tan30°=2,
∴$\overrightarrow{OD}=2\overrightarrow{OA}$,$\overrightarrow{OE}=\frac{4}{3}\overrightarrow{OB}$,
∵$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),又$\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{OE}$=2$\overrightarrow{OA}$+$\frac{4}{3}\overrightarrow{OE}$,
∴$λ=2,μ=\frac{4}{3}$,
∴$\frac{λ}{μ}$=$\frac{2}{\frac{4}{3}}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查向量中两个参数的比值的求法,是中档题,解题时要认真审题,注意向量的线性运算性质的合理运用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 直角或钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
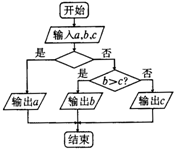
| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com