
已知 的展开式的二项式系数之和为
的展开式的二项式系数之和为 ,且展开式中含
,且展开式中含 项的系数为
项的系数为 .⑴求
.⑴求 的值;⑵求
的值;⑵求 展开式中含
展开式中含 项的系数.
项的系数.
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数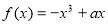 在
在 上是增函数.
上是增函数.
⑴求实数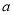 的取值范围
的取值范围 ;
;
⑵当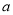 为
为 中最小值时,定义数列
中最小值时,定义数列 满足:
满足: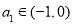 ,且
,且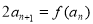 ,
,
用数学归纳法证明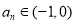 ,并判断
,并判断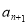 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:(i)
满足:(i) ;(ii)对任意
;(ii)对任意 ,当
,当 时,恒有
时,恒有 .那么称这两个集合“保序同构”.现给出以下4对集合. ①
.那么称这两个集合“保序同构”.现给出以下4对集合. ① ;②
;② ;③
;③ ;④
;④ ,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
,其中,“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com