
已知a,b,c为互不相等的非负数,求证:a2+b2+c2> (
( +
+ +
+ ).
).
见解析
【解析】
试题分析:因为a,b,c为互不相等的非负数,由重要不等式得,a2+b2>2ab,b2+c2>2bc,a2+c2>2ac,利用同向不等式的加法原则得,a2+b2+c2>ab+bc+ac,由基本不等式得ab+bc>2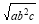 ,bc+ac>2
,bc+ac>2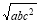 ,ab+ac>2
,ab+ac>2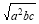 ,再利用加法原则得,ab+bc+ac>
,再利用加法原则得,ab+bc+ac>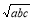 (
(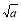 +
+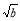 +
+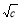 ),再利用不等式的传递性即得所要证明的结论.
),再利用不等式的传递性即得所要证明的结论.
试题解析:证明 ∵a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac.
又∵a,b,c为互不相等的非负数,
∴上面三个式子中都不能取“=”,
∴a2+b2+c2>ab+bc+ac,
∵ab+bc≥2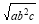 ,bc+ac≥2
,bc+ac≥2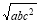 ,
,
ab+ac≥2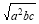 ,
,
又a,b,c为互不相等的非负数,
∴ab+bc+ac>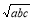 (
(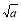 +
+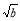 +
+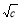 ),
),
∴a2+b2+c2>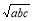 (
(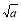 +
+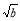 +
+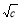 ) (14分)
) (14分)
考点:重要不等式;基本不等式;不等式性质


科目:高中数学 来源:2015届山西省忻州市高二下学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数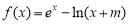 ,其中
,其中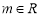 且m为常数.
且m为常数.
(1)试判断当 时函数
时函数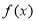 在区间
在区间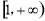 上的单调性,并证明;
上的单调性,并证明;
(2)设函数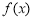 在
在 处取得极值,求
处取得极值,求 的值,并讨论函数
的值,并讨论函数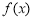 的单调性.
的单调性.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高二下学期期中联考文科数学试卷(解析版) 题型:选择题
已知中心在坐标原点,焦点在 轴上的双曲线
轴上的双曲线 的渐近线方程为
的渐近线方程为 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A. B.
B. C.
C. D.5
D.5
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
只用1,2,3三个数字组成一个四位数,规定这三个数必须同时使用,且同一数字不能相邻出现,这样的四位数有( )
A.6个 B.9个 C.18个 D.36个
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
某小卖部销售一品牌饮料的零售价 (元/评)与销售量
(元/评)与销售量 (瓶)的关系统计如下:
(瓶)的关系统计如下:
零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
已知的关系符合线性回归方程 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考理科数学试卷(解析版) 题型:选择题
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com