
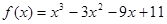
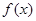 的递减区间;
的递减区间;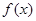 的极大值或极小值,如有试写出极值;
的极大值或极小值,如有试写出极值;科目:高中数学 来源:不详 题型:解答题
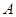 、
、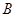 两个项目,预计投资
两个项目,预计投资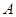 项目
项目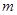 万元可获得利润
万元可获得利润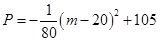
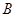 项目
项目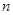 万元可获得利润
万元可获得利润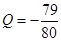
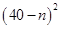
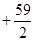
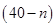 万元.若该企业用40
万元.若该企业用40查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
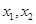 是函数
是函数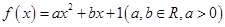 的两个零点,函数
的两个零点,函数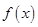 的最小值为
的最小值为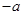 ,记
,记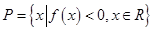
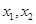 之间的等量关系(不含
之间的等量关系(不含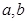 );
);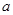 在什么范围内,函数
在什么范围内,函数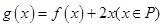 存在最小值?
存在最小值?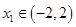 ,试确定
,试确定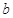 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
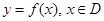 ,若存在常数C,对任意的
,若存在常数C,对任意的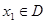 ,存在唯一的
,存在唯一的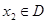 ,使得
,使得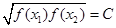 ,则称函数
,则称函数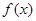 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知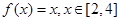 ,则函数
,则函数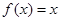 在
在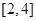 上的几何平均数为( )
上的几何平均数为( ) 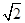 B.
B.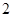 C.
C.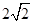 D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
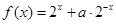 是定义域为
是定义域为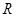 的奇函数,(1)求实数
的奇函数,(1)求实数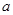 的值;(2)证明
的值;(2)证明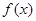 是
是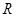 上的单调函数;(3)若对于任意的
上的单调函数;(3)若对于任意的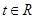 ,不等式
,不等式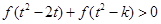 恒成立,求
恒成立,求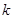 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
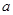 元(一年定期),若年利率为
元(一年定期),若年利率为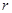 保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为A. | B. | C.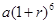 | D.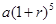 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com