
(1)抛物线的方程;
(2)△AQB的面积的最大值.
解:(1)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),则|AF|=x1+![]() ,|BF|=x2+
,|BF|=x2+![]() .
.
所以|AF|+|BF|=x1+x2+p=8,
即p+2x0=8.①
由y12=2px1,y22=2px2得y12-y22=2p(x1-x2),所以![]() .
.
因为MQ垂直平分AB,所以kMQ=![]() ,又kMQ=
,又kMQ=![]() ,所以
,所以![]() ,
,
所以p=6-x0.②
由①②得x0=2,p=4.
故抛物线的方程为y2=8x.
(2)由(1)知,kAB=![]() ,M(2,y0),所以AB的方程为y-y0=
,M(2,y0),所以AB的方程为y-y0=![]() (x-2),代入y2=8x得y2-2y0y+2y02-16=0,
(x-2),代入y2=8x得y2-2y0y+2y02-16=0,
由Δ>0得-4<y0<4,且y1+y2=2y0,y1y2=2y02-16.
所以|AB|=![]() .
.
所以S△AQB=![]() |AB|·|MQ|
|AB|·|MQ|
=![]()
=![]()
![]()
≤![]() .
.
当且仅当16+y02=32-2y02,即y0=±![]() 时取等号.
时取等号.
故△AQB的面积的最大值为![]() .
.
点拨:运用不等式求最值作为一种思想渗透在各种题型中,经常与其他的知识结合起来考查.因此,一定要掌握不等式的基本性质,并能对其加以灵活运用.


科目:高中数学 来源: 题型:
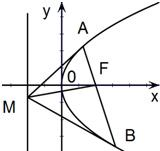 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| FA |
| FB |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
| B、p2 | ||
| C、2p2 | ||
| D、4p2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com