
【题目】(本小题满分14分)
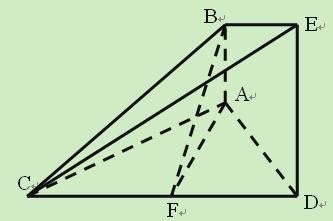
如图的几何体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,△
,△![]() 为等边三角形
为等边三角形![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() 。
。
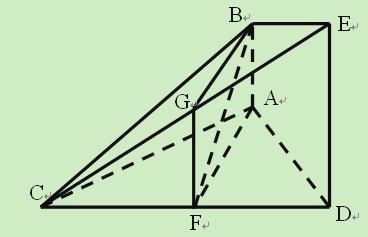
【答案】(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() . …………3分
. …………3分
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .……………5分
.……………5分
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .…………7分
.…………7分
(2)证明:∵![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 的中点,∴
的中点,∴![]() …………9分
…………9分
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() .……………10分
.……………10分
又![]() ,∴
,∴![]() 平面
平面![]() .……………………………12分
.……………………………12分
∵![]() ,∴
,∴![]() 平面
平面![]() .…………………………………13分
.…………………………………13分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .………………14分
.………………14分
【解析】试题分析:(1)通过取![]() 的中点
的中点![]() ,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;(2)连接
,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;(2)连接![]() ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用等体积法
,利用等体积法![]() 可求得结果.
可求得结果.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∴四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)连接![]() ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴由![]() ,即
,即![]() (
(![]() 为正
为正![]() 的高),
的高),
∴![]()
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】某医学院读书协会欲研究昼夜温差大小与患感冒人数多少之间的关系,该协会分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下频数分布直方图:
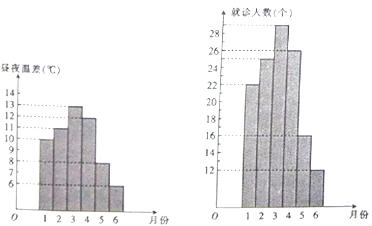
该协会确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的频率;
(2)已知选取的是1月与6月的两组数据.
(i)请根据2至5月份的数据,求出就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程;
的线性回归方程;
(ii)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该协会所得线性回归方程是否理想?
(参考公式: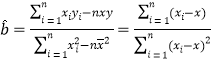 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
频数 | 35 | 20 | 25 | 20 |
支持脱欧的人数 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持“脱欧”人数 | |||
不支持“脱欧”人数 | |||
合计 |
附:![]()

(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元)。
(单位:万元)。
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.
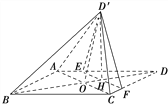
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱锥D′ABCFE的体积.
,求五棱锥D′ABCFE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com