
选修4-4:坐标系与参数方程
在以直角坐标原点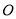 为极点,
为极点,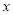 的非负半轴为极轴的极坐标系下,曲线
的非负半轴为极轴的极坐标系下,曲线 的方程是
的方程是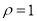 ,将
,将 向上平移1个单位得到曲线
向上平移1个单位得到曲线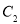 .
.
(1)求曲线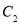 的极坐标方程;
的极坐标方程;
(2)若曲线 的切线交曲线
的切线交曲线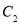 于不同两点
于不同两点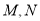 ,切点为
,切点为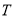 .求
.求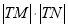 的取值范围.
的取值范围.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:2017届河南息县第一高级中学高三上阶段测三数学(文)试卷(解析版) 题型:解答题
设函数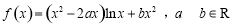 .
.
(Ⅰ)当 时,求曲线
时,求曲线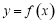 在点
在点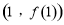 处的切线方程;
处的切线方程;
(Ⅱ)当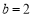 时,若对任意
时,若对任意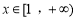 ,不等式
,不等式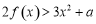 恒成立,求实数
恒成立,求实数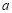 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期一调考试数学(文)试卷(解析版) 题型:选择题
设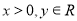 ,则“
,则“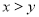 ”是“
”是“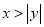 ”的( )
”的( )
A. 充要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期一调考试数学(理)试卷(解析版) 题型:选择题
已知命题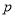 :方程
:方程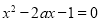 有两个实数根;命题
有两个实数根;命题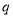 :函数
:函数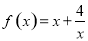 的最小值为
的最小值为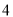 .给出下列命题:
.给出下列命题:
①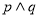 ;②
;② ;③
;③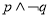 ;④
;④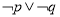 .
.
则其中真命题的个数为( )
A. B.
B.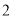 C.
C.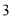 D.
D.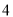
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁瓦房店市高二下期末数学(文)试卷(解析版) 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁瓦房店市高二下期末数学(文)试卷(解析版) 题型:选择题
已知向量 为平面向量,若
为平面向量,若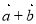 与
与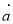 的夹角为
的夹角为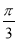 ,
,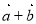 与
与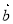 的夹角为
的夹角为 ,则
,则 ( )
( )
A.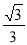 B.
B.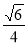 C.
C.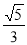 D.
D.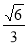
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁瓦房店市高二下期末数学(理)试卷(解析版) 题型:解答题
某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如下频率分布直方图.
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为 ,求
,求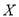 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁省协作校高二下期末数学(文)试卷(解析版) 题型:选择题
若集合A={x|(x-1)2<4},B={x||x|>1}则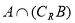 =( )
=( )
A.{x|-1<x≤1} B.{x|-1≤x<1}
C.{x|-1≤x≤1} D.{x|-1<x<1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com