
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| x1 |
| 1 |
| 2 |
| 4x2 |
| x1 |
| 1 |
| 2 |
| 4x2 |
| x1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| x1 |
| 1 |
| 2 |
| 4x2 |
| x1 |
| 1 |
| 2 |
| 4x2 |
| x1 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4x2 |
| x1 |
| 3 |
| 2 |
| 3 |
| 2 |
|


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| OE |
| 1 |
| 2 |
| OF |
| OA |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、n⊥α,n⊥β,m⊥α |
| B、α∩γ=m,α⊥γ,β⊥γ |
| C、α⊥γ,β⊥γ,m⊥α |
| D、α⊥β,α∩β=l,m⊥l |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
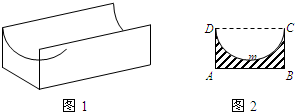 图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.设AB=2x,BC=y,凹槽的强度与横截面的面积的x倍成正比,且当AB=1时凹槽的强度为| 4-π |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| AB |
| AC |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 平面 | 空间 |
| 三角形的两边之和大于第三边 | 四面体的任意三个面的面积之和大于第四个面的面积 |
| 三角形的面积等于任意一边的长度与这个边上高的乘积的二分之一 | 四面体的体积等于任意底面的面积与这个底面上的高的乘积的三分之一 |
| 三角形的面积等于其内切圆的半径与三角形周长乘积的二分之一 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com