
设函数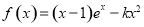 (其中
(其中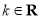 ).
).
(1) 当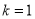 时,求函数
时,求函数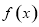 的单调区间;
的单调区间;
(2) 当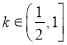 时,求函数
时,求函数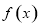 在
在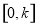 上的最大值
上的最大值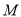 .
.
(1) 函数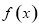 的递减区间为
的递减区间为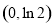 ,递增区间为
,递增区间为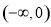 ,
,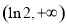 ;
;
(2) 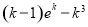
【解析】
试题分析:(1)由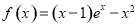
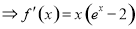 ,利用导数的符号判断函数
,利用导数的符号判断函数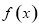 的单调性和求单调区间;
的单调性和求单调区间;
(2)
试题解析:
【解析】
(1)当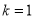 时,
时,
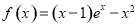 ,
,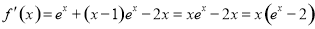
令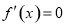 ,得
,得 ,
,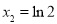
当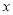 变化时,
变化时,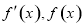 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
右表可知,函数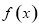 的递减区间为
的递减区间为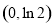 ,递增区间为
,递增区间为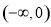 ,
,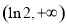 .
.
(2) 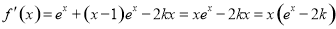 ,令
,令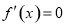 ,得
,得 ,
,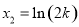 , 令
, 令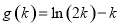 ,则
,则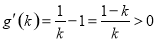 ,所以
,所以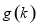 在
在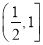 上递增, 所以
上递增, 所以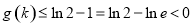 ,从而
,从而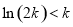 ,所以
,所以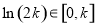
所以当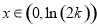 时,
时,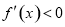 ;当
;当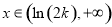 时,
时,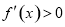 ;
;
所以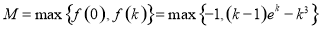
令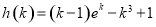 ,则
,则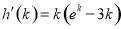 ,令
,令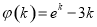 ,则
,则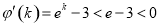
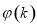 在
在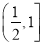 上递减,而
上递减,而
所以存在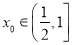 使得
使得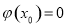 ,且当
,且当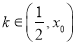 时,
时,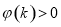 当
当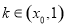 时,
时,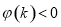
所以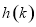 在
在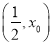 上单调递增,在
上单调递增,在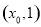 上单调递减.
上单调递减.
因为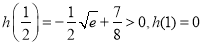 ,所以
,所以 在
在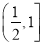 上恒成立,当且仅当
上恒成立,当且仅当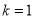 时取得“=”.综上,函数
时取得“=”.综上,函数 在
在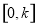 上的最大值
上的最大值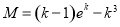 .
.
考点:1、导数在研究函数性质中的综合应用;2、等价转化的思想.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试文科数学试卷(A)(解析版) 题型:选择题
设 ,
, 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是 ( )
的解集是 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:
①垂直于同一条直线的两条直线互相平行
②垂直于同一个平面的两条直线互相平行
③垂直于同一条直线的两个平面互相平行
④垂直于同一个平面的两个平面互相平行,则正确的结论是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二普通班上学期期中理科数学试卷(解析版) 题型:选择题
设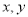 满足约束条件
满足约束条件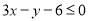 ,
,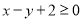 ,
,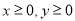 ,若目标函数
,若目标函数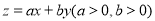 的最大值为12,则
的最大值为12,则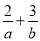 的最小值为( )
的最小值为( )
A.5 B.6 C.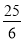 D.
D.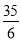
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二普通班上学期期中理科数学试卷(解析版) 题型:选择题
在△ABC中,sin2A=sin2B+sin2C,则△ABC为( )
A.直角三角形 B.等腰直角三角形
C.等边三角形 D.等腰三角形
查看答案和解析>>
科目:高中数学 来源:2015届河南省高二实验班上学期期中考试数学试卷(解析版) 题型:选择题
设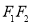 是椭圆
是椭圆 的左、右焦点,
的左、右焦点,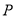 为直线
为直线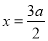 上一点,
上一点, 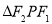 是底角为
是底角为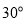 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
(A)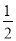 (B)
(B)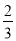 (C)
(C) (D)
(D)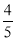
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com