
(本题满分12分)F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.(Ⅰ)根据条件求出b和k满足的关系式;(Ⅱ)向量![]() 在向量
在向量![]() 方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(Ⅰ) b2=2(k2+1) (k??±1,b>0) (Ⅱ) y=±x+ (Ⅲ)[3]
:(Ⅰ)b和k满足的关系式为b2=2(k2+1) (k??±1,b>0)………3分
(Ⅱ)设A(x1,y1) B(x2,y2),则由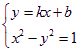 消去y得(k2-1)x2+2kbx+b2+1=0,其中k2??1……4分
消去y得(k2-1)x2+2kbx+b2+1=0,其中k2??1……4分
∴×=x1x2+y1y2=(1+k2)x1x2+kb(x1+x2)+b2= + + 2(k2+1)
由于向量![]() 方向上的投影是p∴p2=cos2<,
方向上的投影是p∴p2=cos2<,![]() >= …6分
>= …6分
∴(×)×p2= + +2=1??k=±∵b2= 2(k2+1) (k??±1,b>0), 故b= ,经检验适合D>0
∴直线l的方程为y=±x+ …………8分
(Ⅲ)类似于(Ⅱ)可得+ +2=m∴k2=1+ , b2=4+ 根据弦长公式
得![]() …10分
…10分
则SDAOB= |AB|×=而m??[2,4],∴DAOB的面积的取值范围是[3] 12分


科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
如图,斜率为1的直线![]() 过抛物线
过抛物线![]() 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。
(1)若|AB|=8,求抛物线![]() 的方程;
的方程;
(2)设C为抛物线弧AB上的动点(不包括A,B两点),求![]() 的面积S的最大值;
的面积S的最大值;
(3)设P是抛物线![]() 上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)
上异于A,B的任意一点,直线PA,PB分别交抛物线的准线于M,N两点,证明M,N两点的纵坐标之积为定值(仅与p有关)

查看答案和解析>>
科目:高中数学 来源:2012年吉林省高一第一次月考数学 题型:解答题
(本题满分12分)已知函数f(x)=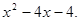
(1)若函数定义域为[3,4],求函数值域
(2)若函数定义域为[-3,4],求函数值域
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期期中考试文科数学 题型:解答题
(本题满分12分)已知函数f(x)=cos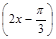 +2sin
+2sin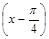 ·sin
·sin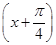 .
.
(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间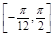 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源:重庆市09-10学年高二下学期5月月考(数学文) 题型:解答题
(本题满分12分)如图,正四棱柱ABCD—A1B1C1D1中,底面边长为 ,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
(1)求证:B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1—EFD1的体积V.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com