甲.乙两艘轮船驶向一个不能同时停泊两艘轮船的码头.它们在一昼夜内任何时刻到达是等可能的．如果甲船和乙船的停泊时间都是4小时.求它们中的任何一条船不需要等待码头空出的概率．题目和参考答案——青夏教育精英家教网—

10．甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内任何时刻到达是等可能的．如果甲船和乙船的停泊时间都是4小时，求它们中的任何一条船不需要等待码头空出的概率．

分析如果甲船和乙船的停泊时间都是4小时，设甲、乙两船到达时间分别为x、y，我们可以画出（x，y）点对称的平面区域，及满足条件y-x＞4或y-x＜-4平面区域，分别求出对应面积，代入几何概型公式，即可求出答案．

解答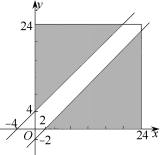解：设甲、乙两船到达时间分别为x、y，
则0≤x＜24，0≤y＜24且y-x≥4或y-x≤-4．
作出区域y-x＞4或y-x＜-4.0≤y＜24，
设“两船无需等待码头空出”为事件A，
则P（A）=$\frac{\frac{1}{2}×2×20×20}{24×24}$=$\frac{25}{36}$．

点评本题考查的知识点是几何概型，其中求出所有基本事件对应的平面区域的面积，及满足条件的平面区域的面积是解答本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

18．《聊斋志异》中有这样一首诗：“挑水砍柴不堪苦，请归但求穿墙术．得诀自诩无所阻，额上坟起终不悟．”在这里，我们称形如以下形式的等式具有“穿墙术”：
2$\sqrt{\frac{2}{3}}$=$\sqrt{2\frac{2}{3}}$，3$\sqrt{\frac{3}{8}}$=$\sqrt{3\frac{3}{8}}$，4$\sqrt{\frac{4}{15}}$=$\sqrt{4\frac{4}{15}}$，5$\sqrt{\frac{5}{24}}$=$\sqrt{5\frac{5}{24}}$
则按照以上规律，若8$\sqrt{\frac{8}{n}}$=$\sqrt{8\frac{8}{n}}$具有“穿墙术”，则n=（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．

如图，正三棱柱ABC-A₁B₁C₁（底面是正三角形，侧棱垂直底面）的各条棱长均相等，D为AA₁的中点．M、N分别是BB₁、CC₁上的动点（含端点），且满足BM=C₁N．
当M、N运动时，下列结论中正确的是①②④（填上所有正确命题的序号）．
①平面DMN⊥平面BCC₁B₁；
②三棱锥A₁-DMN的体积为定值；
③△DMN可能为直角三角形；
④平面DMN与平面ABC所成的锐二面角范围为$（0，\frac{π}{4}]$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．设曲线y=xⁿ⁺¹（n∈N^*）在点（1，1）处的切线与x轴的交点横坐标为x_n，则log₂₀₁₂x₁+log₂₀₁₂x₂+…+log₂₀₁₂x₂₀₁₂的值为（　　）

A．

-log₂₀₁₂2011

B．

-1

C．

-1+log₂₀₁₂2011

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．给出如下列联表（公式见卷首）

	患心脏病	患其它病	合计
高血压	20	10	30
不高血压	30	50	80
合计	50	60	110

P（K²≥10.828）≈0.001，P（K²≥6.635）≈0.010
参照公式，得到的正确结论是（　　）

	A．	有99%以上的把握认为“高血压与患心脏病无关”
	B．	有99%以上的把握认为“高血压与患心脏病有关”
	C．	在犯错误的概率不超过0.1%的前提下，认为“高血压与患心脏病无关”
	D．	在犯错误的概率不超过0.1%的前提下，认为“高血压与患心脏病有关”

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．由曲线y=sinx-$\sqrt{3}$cosx与直线y=0，x=$\frac{2π}{3}$，x=π所围成的图形的面积S是2．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

2．若函数$f（x）=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}-mx+8$存在极值，则m的取值范围是m＞$-\frac{1}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．函数y=$\sqrt{1-x}$+$\sqrt{2x}$的定义域为（　　）

A．

（-∞，1]

B．