
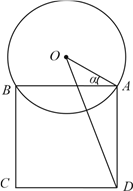
【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设![]() .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)
(1)用![]() 表示圆柱的高;
表示圆柱的高;
(2)实践表明,当球心![]() 和圆柱底面圆周上的点
和圆柱底面圆周上的点![]() 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效
果最佳,求此时![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]()
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两个不同点,求
两个不同点,求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 有无数对互相垂直的直线
有无数对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的一系列对应值如表:
)的一系列对应值如表:

(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果:
①当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为![]() 的圆的圆心在
的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线![]()
![]() 与圆相交于
与圆相交于![]() 两点,求实数
两点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(﹣1,1)的密度曲线)的点的个数的估计值为( ) 附:若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.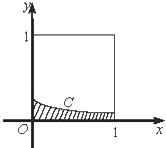
A.1 193
B.1 359
C.2 718
D.3 413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
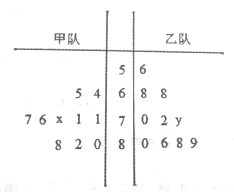
(1)求![]() 的值;(直接写出结果,不必写过程)
的值;(直接写出结果,不必写过程)
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com