
 (万元)的关系,有经验公式
(万元)的关系,有经验公式 ,今有3万元资金投入经营甲、乙两种商品,对甲、乙两种商品的资金投入应分别为多少时,才能获得最大利润?
,今有3万元资金投入经营甲、乙两种商品,对甲、乙两种商品的资金投入应分别为多少时,才能获得最大利润?科目:高中数学 来源:不详 题型:单选题
 ,这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是:( )
,这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是:( )| A.它没有单调性 | B.它是周期函数,且没有最小正周期 |
| C.它是偶函数 | D.它有函数图像 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
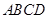 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕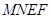 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形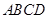 是边长为30米的正方形,电源在点
是边长为30米的正方形,电源在点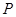 处,点
处,点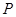 到边
到边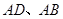 的距离分别为9米,3米,且
的距离分别为9米,3米,且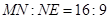 ,线段
,线段 必过点
必过点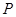 ,端点
,端点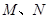 分别在边
分别在边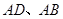 上,设
上,设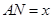 米,液晶广告屏幕
米,液晶广告屏幕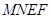 的面积为
的面积为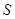 平方米.
平方米.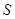 关于
关于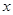 的函数关系式及其定义域;
的函数关系式及其定义域;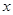 为何值时,液晶广告屏幕
为何值时,液晶广告屏幕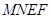 的面积
的面积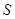 最小?
最小?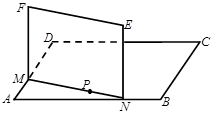
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com