
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 点
点 km,乙离
km,乙离 点
点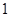 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行. 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
科目:高中数学 来源:不详 题型:单选题
 =Asin(ωx+ф)(A>0,ω>0)的图像在y轴右侧的第一个最高点为M(2,2),与x轴在原点右侧的第一个交点为N(5,0),则函数
=Asin(ωx+ф)(A>0,ω>0)的图像在y轴右侧的第一个最高点为M(2,2),与x轴在原点右侧的第一个交点为N(5,0),则函数 的解析式为
的解析式为 A.2sin(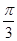 x+ x+ ) ) | B.2sin(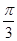 x- x- ) ) |
C.2sin( x+ x+ ) ) | D.2sin( x+ x+ ) ) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是函数
是函数 的一个对称中心;②若
的一个对称中心;②若 是第一象限角,且
是第一象限角,且 ,则
,则 ;③函数
;③函数 是偶函数;④定义平面向量之间的一种新运算“
是偶函数;④定义平面向量之间的一种新运算“ ”如下:对任意的
”如下:对任意的 ,
, ,若
,若


 ,则
,则




 ;其中正确命题的序号是( )
;其中正确命题的序号是( )| A.①③④ | B.①③ | C.②③④ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
). ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间; ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com