
 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
). ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间; ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.  +2kπ,
+2kπ, +2kπ](k∈Z)
+2kπ](k∈Z)
 ·
· 得
得 +sin
+sin )·(cos
)·(cos -sin
-sin )+(-sin
)+(-sin )·2cos
)·2cos
 -sin2
-sin2 -2sin
-2sin cos
cos =cosx-sinx=
=cosx-sinx= cos(x+
cos(x+ ),...........4分
),...........4分 ≤π+2kπ,k∈Z,
≤π+2kπ,k∈Z, +2kπ≤x≤
+2kπ≤x≤ +2kπ,k∈Z.
+2kπ,k∈Z. +2kπ,
+2kπ, +2kπ](k∈Z) ……..8分
+2kπ](k∈Z) ……..8分 cos(x+
cos(x+ )=1,故cos(x+
)=1,故cos(x+ )=
)= ……10分
……10分 ,于是有x+
,于是有x+ ∈
∈ ,得x1=0,x2=-
,得x1=0,x2=- ,
,


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:不详 题型:解答题
 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 点
点 km,乙离
km,乙离 点
点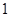 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行. 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com