
|
|
|
| α |
| α |
| α |
| m |
| m |
| m |
|
|
|
|
|
|
|
|
| m |
|
|
|
|
|
| m |
| m |
| λ | 4 2 |
|
|
|


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
 (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲
|
|
| π |
| 3 |
| 1 |
| abc |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省海安高级中学、南京外国语学校、金陵中学高三调研数学试卷(解析版) 题型:解答题
 ,
, ,求满足AX=B的二阶矩阵X.
,求满足AX=B的二阶矩阵X. ),它们相交于A,B两点,求线段AB的长.
),它们相交于A,B两点,求线段AB的长. ≥2
≥2 .
.
查看答案和解析>>
科目:高中数学 来源:江苏省2010届三校四模联考 题型:解答题
【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4 – 1几何证明选讲
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,
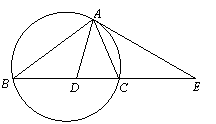 ∠BAC的平分线与BC交于点D.
∠BAC的平分线与BC交于点D.
求证:ED2= EB·EC.
B.矩阵与变换
已知矩阵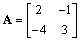 ,
,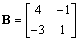 ,求满足
,求满足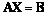 的二阶矩阵
的二阶矩阵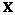 .
.
C.选修4 – 4 参数方程与极坐标
若两条曲线的极坐标方程分别为r = 1与r = 2cos( + ),它们相交于A,B两点,求线段AB的长.
D.选修4 – 5 不等式证明选讲
设a,b,c为正实数,求证:a3 + b3 + c3 + ≥2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com