
在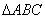 ,内角
,内角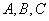 所对的边长分别为
所对的边长分别为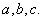
 且
且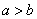 ,则
,则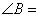 ________.
________.
科目:高中数学 来源: 题型:
在数列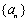 中,已知
中,已知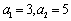 ,其前n项和
,其前n项和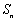 满足
满足
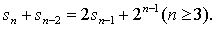 .
.
(1) 求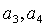 的值;
的值;
(2)求数列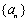 的通项公式
的通项公式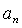 ;
;
(3)令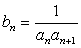 ,试求一个函数
,试求一个函数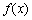 ,使得对于任意正整数n有
,使得对于任意正整数n有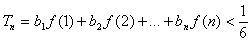 ,且对于任意的
,且对于任意的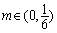 ,均存在
,均存在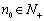 ,使得
,使得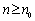 时,
时,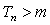 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
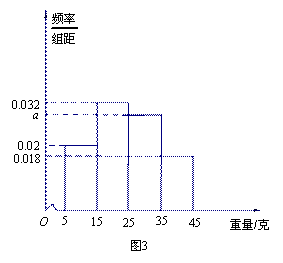
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为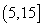 ,
,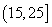 ,
,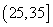 ,
,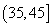 ,由此得到重量样本的频率分布直方图,如图3.
,由此得到重量样本的频率分布直方图,如图3.
(1)求 的值;
的值;
(2)若重量在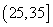 ,
,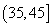 中采用分层抽样方法抽出8尾作为特别实验,那么在
中采用分层抽样方法抽出8尾作为特别实验,那么在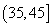 中需取出几尾?
中需取出几尾?
(3)从大量马口鱼中机抽取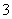 尾,其中重量在
尾,其中重量在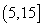 内的尾数为
内的尾数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
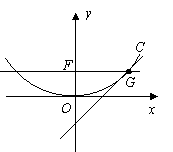
设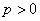 ,抛物线方程为
,抛物线方程为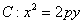 .如图所示,过焦点
.如图所示,过焦点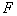 作
作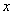 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为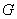 ,已知抛物线在点
,已知抛物线在点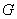 的切线经过点
的切线经过点 .
.
(1)求满足条件的抛物线方程;
(2)过点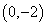 作抛物线
作抛物线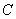 的切线,若切点在第二象限,求切线
的切线,若切点在第二象限,求切线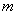 的方程;
的方程;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com