
(本题满分14分)已知函数f(x)=ax2-|x|+2a-1(a为实常数).
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设h(x)= ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
(1)见解析(2)  (3)
(3)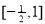
【解析】
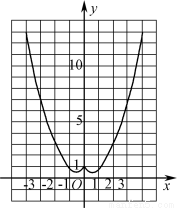
试题分析:(1)当a=1时化简函数式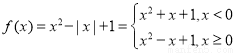 ,由此可画出图像如下
,由此可画出图像如下
(2)当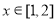 时,
时,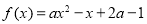 ,对a加以讨论,分
,对a加以讨论,分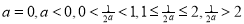 这几种情况,结合图像,利用单调性可得
这几种情况,结合图像,利用单调性可得
(3) 当x∈[1,2]时,依题意h(x)=ax+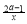 -1,h(x)在区间[1,2]上是增函数,由函数单调性定义可得
-1,h(x)在区间[1,2]上是增函数,由函数单调性定义可得
在区间[1,2]上任取x1,x2,且x1<x2,
则h(x2)-h(x1) =(x2-x1) >0,
>0,
因为x2-x1>0,x1x2>0,所以ax1x2-(2a-1)>0,即ax1x2>2a-1,对a分情况讨论得:
当a=0时,上面的不等式变为0>-1,即a=0时结论成立.
当a>0时,x1x2>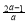 ,由1<x1x2<4得,
,由1<x1x2<4得,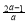 ≤1,解得0<a≤1,
≤1,解得0<a≤1,
当a<0时,x1x2<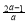 ,由1<x1x2<4得,
,由1<x1x2<4得,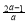 ≥4,解得
≥4,解得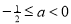
综上,实数a的取值范围为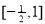
试题解析: (1)当a=1时,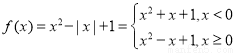
作图(如图所示)

(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,g(a)=f(2)=-3.
若a≠0,则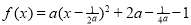 ,f(x)图象的对称轴是直线x=
,f(x)图象的对称轴是直线x=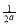
当a<0时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
当0<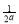 <1,即a>
<1,即a>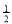 时,f(x)在区间[1,2]上是增函数,g(a)=f(1)=3a-2.
时,f(x)在区间[1,2]上是增函数,g(a)=f(1)=3a-2.
当1≤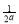
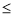 2,即
2,即 ≤a≤
≤a≤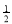 时,g(a)=f(
时,g(a)=f(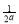 )=
)=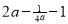
当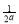 >2,即0<a<
>2,即0<a<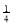 时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
综上可得
(3)当x∈[1,2]时,h(x)=ax+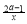 -1,在区间[1,2]上任取x1,x2,且x1<x2,
-1,在区间[1,2]上任取x1,x2,且x1<x2,
则h(x2)-h(x1)=(ax2+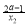 -1)-(ax1+
-1)-(ax1+ -1)=(x2-x1)(a-
-1)=(x2-x1)(a-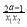 )=(x2-x1)
)=(x2-x1)
因为h(x)在区间[1,2]上是增函数,所以h(x2)-h(x1)>0,
因为x2-x1>0,x1x2>0,所以ax1x2-(2a-1)>0,即ax1x2>2a-1,
当a=0时,上面的不等式变为0>-1,即a=0时结论成立.
当a>0时,x1x2>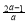 ,由1<x1x2<4得,
,由1<x1x2<4得,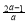 ≤1,解得0<a≤1,
≤1,解得0<a≤1,
当a<0时,x1x2<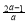 ,由1<x1x2<4得,
,由1<x1x2<4得,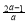 ≥4,解得
≥4,解得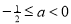
综上,实数a的取值范围为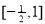
考点:含绝对值的函数的图像和性质及分类讨论思想.


科目:高中数学 来源:2014-2015学年广东省高一第一次月考数学试卷(解析版) 题型:选择题
设集合A={x|1<x≤2},B={ x|x<a},若A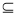 B,则a的取值范围是( ).
B,则a的取值范围是( ).
A.a≥1 B.a≤1 C.a>2 D.a≥2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com