���𰸡�
����������Բ�ı����̵ĸ���ɵã�1������ȷ������Բ���е�������ֱ�߷�����ʽ���ɵã�2����ȷ�����ݹ�Բ��һ�����������Բ�����ߣ��ɵã�3������ȷ������Բ�ĵĹ켣���̡��㵽ֱ�ߵľ��빫ʽ�����ֱ����Բ��λ�ù�ϵ�õ���4����ȷ������ֱ�ߵ�n=4��m=0ʱ��ֱ��kx-y+1-2k=0����ԲC�ڲ�һ�㣬�ɵã�5������ȷ��
����⣺���ڣ�1������m=1ʱ������C����x-1��
2+��y-2��
2=
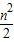
��
��n��0ʱ����ʾԲ��Ϊ��1��2�����뾶Ϊ
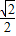
|n|��Բ��
��������ȱ����n��0���ʣ�1������ȷ��
���ڣ�2������m=0��n=2ʱ������C��x
2+y
2=2����ʾԲ����ԭ��뾶Ϊ
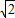
��Բ
��A��x
1��y
1����B��x
2��y
2�����ɵ�
�߾�����A��Բ������Ϊx
1x+y
1y=2��������B��Բ������Ϊx
2x+y
2y=2��
���ɵ㣨3��3���ֱ������������ϣ���3x
1+3y
1=2��3x
2+3y
2=2����
�ɵþ���A��B��ֱ�߷���Ϊ3x+3y=2����3x+3y-2=0���ʣ�2����ȷ��
���ڣ�3������m=1��n=
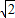
ʱ������C����x-1��
2+��y-2��
2=1��
��ʾԲ����ԭ��1��2�����뾶Ϊ1��Բ
���㣨2��0��������C�����ߣ����߷���Ϊy=-

��x-2����x=2��
���������ߣ��ʣ�3������ȷ��
���ڣ�4������n=m��0ʱ����ΪԲC��ԲC��m��2m������y=2x
��ֱ��x-y=0��y-7x=0������C��ֱ�ߵľ���ǡ�õ���Բ�İ뾶
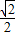
|n|
������C��ʾԲ����ֱ��y=2x�ϵ�Բϵ������ЩԲ�Ĺ����߷���Ϊy=x��y=7x���ã�4����ȷ��
���ڣ�5������n=4��m=0ʱ������C��x
2+y
2=8����ʾԲ����ԭ��뾶Ϊ2
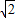
��Բ
ֱ��kx-y+1-2k=0�������㣨2��1����ǡ��ΪԲ��һ��
��ԲC�ض���ֱ���ཻ���ʣ�5������ȷ
�ʴ�Ϊ����2����4��
����������������в�����Բ���̣��жϹ���Բ���̵ļ������۵���ȷ�ԣ����ؿ�����Բ�ı����̡��㵽ֱ�ߵľ��빫ʽ��ֱ����Բ��λ�ù�ϵ��֪ʶ�㣬�����е��⣮

 ��������������ۣ�
��������������ۣ� |n|��Բ��
|n|��Բ�� ʱ�����㣨2��0��������C�����ߣ������߷���Ϊy=-
ʱ�����㣨2��0��������C�����ߣ������߷���Ϊy=- ��x-2����
��x-2����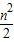 ��
��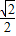 |n|��Բ��
|n|��Բ��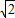 ��Բ
��Բ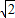 ʱ������C����x-1��2+��y-2��2=1��
ʱ������C����x-1��2+��y-2��2=1�� ��x-2����x=2��
��x-2����x=2��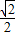 |n|
|n|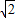 ��Բ
��Բ


 ��Բx2+y2=4������һ��P��x��Ĵ��ߣ�����ΪQ����M���߶�PQ�ϣ���
��Բx2+y2=4������һ��P��x��Ĵ��ߣ�����ΪQ����M���߶�PQ�ϣ���