
设函数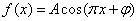 (其中
(其中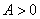 ,
, ,
, ).当
).当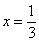 时,
时,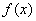 取得最小值
取得最小值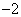 .
.
(1)求函数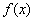 的解析式;
的解析式;
(2)求函数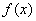 的单调递增区间.
的单调递增区间.
科目:高中数学 来源: 题型:
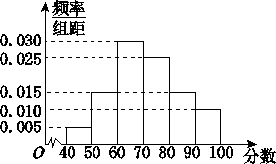
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
下表是抽测某校初二女生身高情况所得的部分资料(身高单位:cm,测量时精确到1cm).已知身高在151cm 以下(含151cm)的被测女生共3人.则所有被测女生总数为 .
| 分组 | [145.5,148.5) | [148.5,151.5) | [151.5,154.5) | [154.5,157.5) | [157.5,160.5) | [160.5,163.5) | [163.5,166.5) | [166.5,169.5] |
| 频率 | 0.02 | 0.04 | 0.08 | 0.12 | 0.30 | 0.20 | 0.18 | 0.06 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com