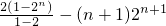Question

各项均为正数的数列{a_n}的前n项和为S_n，满足2（S_n+1）=a_n²+a_n（n∈Nⁿ）（I）求数列{a_n}的通项公式；（II）记b_n=2ⁿa_n，求数列{b_n}的前项和T_n．

Answer 1

解：（I）令n=1，则2（S₁+1）=a₁²+a₁
∴a₁=-1（舍）或a₁=2
当n≥2时，2（S_n+1）=a_n²+a_n
2（S_n-1+1）=a_n-1²+a_n-1
两式相减得
2a_n=a_n²-a_n-1²+a_n-a_n-1
∵a_n＞0
∴a_n-a_n-1=1
∴数列{a_n}为等差数列，首项为2，公差为1
∴a_n=n+1
（II）∵b_n=2ⁿ•a_n=（n+1）•2ⁿ
∴T_n=2•2+3•2²+4•2³+…+n•2^n-1+（n+1）•2ⁿ
2T_n=2•2²+3•2³+…+n•2ⁿ+（n+1）•2ⁿ⁺¹
两式相减得
-T_n=2+2+2²+2³+…+2ⁿ-（n+1）•2ⁿ⁺¹
=2+
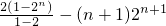
∴T_n=n•2ⁿ⁺¹
分析：（I）通过仿写作差将和与项的递推关系转化为项间的递推关系，利用等差数列的定义判断出数列{a_n}为等差数列，利用等差数列的通项公式求出通项．
（II）求出数列{b_n}的通项，据通项特点，选择利用错位相减法求数列的前n项和．
点评：求数列的前n项和，首先求出数列的通项，根据通项的特点选择合适的求和方法，当通项是一个等差数列与等比数列的乘积构成的新数列，利用错位相减法求和．