
思路解析:本题中条件有两个方面,一方面是耕地面积每年新增100亩,土地的亩数按年份排起来是等差数列.另一方面,人口以1%的增长率增长,人口数按年份排起来是等比
数列.利用等差和等比数列的知识可解本题.
解:由已知得,自2003年年底起,每年年底的耕地面积组成一个等差数列,其首项是30 000,公差d=100.因此,2020年年底的耕地面积是
a18=30 000+17×100=31 700(亩).
自2003年年底起,每年年底的人口数是一个公比q=1.01,首项为30 000的等比数列.那么,2020年年底该乡的人口数为b18=30 000×1.0117=35 529(人).
故到2020年年底该乡人均占有耕地31 700÷35 529≈0.89(亩).
答:到2020年年底该乡人均占有耕地为0.89亩.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
| 时间 | 该林区原有林地减少后的面积 | 该年开荒 造林面积 |
| 2003年年底 | 99.8000万公顷 | 0.3000万公顷 |
| 2004年年底 | 99.6000万公顷 | 0.3000万公顷 |
| 2005年年底 | 99.4001万公顷 | 0.2999万公顷 |
| 2006年年底 | 99.1999万公顷 | 0.3001万公顷 |
| 2007年年底 | 99.0002万公顷 | 0.2998万公顷 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修1) 2009-2010学年 第11期 总167期 人教课标高一版 题型:044
某地区2003年年底的绿化面积为95万公顷,之后五年采取了退耕还林、植树造林的措施,该地区的绿化情况如下表所示:
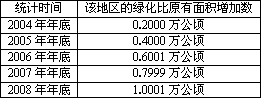
若继续采取这项植树造林的措施,那么到2018年年底,该地区的绿化面积将大约变为多少万公顷?
查看答案和解析>>
科目:高中数学 来源:2007年江苏省南通市高三数学押题卷(35题)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com