
| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
分析 由已知得$\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$=$\overrightarrow{0}$,则$\frac{1}{5}\overrightarrow{OA}+\overrightarrow{OD}$=$\overrightarrow{0}$,从而得到$\overrightarrow{OA}+5\overrightarrow{OD}$=$\overrightarrow{0}$,由此能求出2$\overrightarrow{DB}$+3$\overrightarrow{DC}$=$\overrightarrow{0}$.
解答 解:∵△ABC内一点O满足$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,直线AO交BC于点D,
∴$\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$=$\overrightarrow{0}$,
令$\overrightarrow{OE}$=$\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$,则$\frac{1}{5}\overrightarrow{OA}+\overrightarrow{OD}$=$\overrightarrow{0}$,
∴B,C,E三点共线,A,O,E三点共线,∴D,E重合.
∴$\overrightarrow{OA}+5\overrightarrow{OD}$=$\overrightarrow{0}$,∴2$\overrightarrow{DB}$+3$\overrightarrow{DC}$=2$\overrightarrow{OB}$-2$\overrightarrow{OD}$+3$\overrightarrow{OC}$-3$\overrightarrow{OD}$=-$\overrightarrow{OA}$-5$\overrightarrow{OD}$=$\overrightarrow{0}$.
故选:A.
点评 本题考查命题真假的判断,是基础题,解题时要认真,注意平面向量运算法则的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得f(x)<0 | |
| B. | ?x∈[0,+∞),f(x)≥0 | |
| C. | ?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$ | |
| D. | ?x1∈[0,+∞),?x2∈[0,+∞)使得f(x1)>f(x2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{π}{4}+kπ,\frac{π}{4}+kπ}](k∈Z)$ | B. | $[{\frac{π}{4}+kπ,\frac{3π}{4}+kπ}](k∈Z)$ | ||
| C. | $[{\frac{π}{12}+kπ,\frac{7π}{12}+kπ}](k∈Z)$ | D. | $[{-\frac{5π}{12}+kπ,\frac{π}{12}+kπ}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
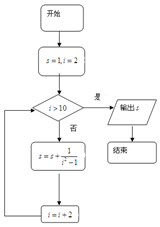
| A. | $\frac{5}{11}$ | B. | $\frac{13}{9}$ | C. | $\frac{16}{11}$ | D. | $\frac{17}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com