
| A. | ?x0∈R,使得f(x)<0 | |
| B. | ?x∈[0,+∞),f(x)≥0 | |
| C. | ?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$ | |
| D. | ?x1∈[0,+∞),?x2∈[0,+∞)使得f(x1)>f(x2) |
分析 函数$f(x)={x^{\frac{1}{2}}}$的值域为[0,+∞),是增函数,由此能求出结果.
解答 解:由函数$f(x)={x^{\frac{1}{2}}}$,知:
在A中,f(x)≥0恒成立,故A错误;
在B中,?x[(0,+∞),f(x)≥0,故B正确;
在C中,?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$>0,故C错误;
在D中,当x1=0时,不存在x2∈[0,+∞)使得f(x1)>f(x2),故D不成立.
故选:B.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意幂函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
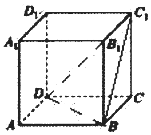 在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )
在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 294 | B. | 174 | C. | 470 | D. | 304 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com