
【题目】(本小题满分16分)已知![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,令
时,令![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
【答案】(1)![]() 的极小值为
的极小值为![]() ,无极大值.(2)
,无极大值.(2)![]()
【解析】
试题分析:(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,由
,由![]() 得
得![]() .列表分析得
.列表分析得![]() 的极小值为
的极小值为![]() ,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化:
,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化:![]() 在
在![]() 上恒成立.由于
上恒成立.由于![]() 不易求,因此再进行转化:当
不易求,因此再进行转化:当![]() 时,
时, ![]() 可化为
可化为![]() ,令
,令![]() ,问题转化为:
,问题转化为:![]() 对任意
对任意![]() 恒成立;同理当
恒成立;同理当![]() 时,
时,![]() 可化为
可化为![]() ,令
,令![]() ,问题转化为:
,问题转化为:![]() 对任意的
对任意的![]() 恒成立;以下根据导函数零点情况进行讨论即可.
恒成立;以下根据导函数零点情况进行讨论即可.
试题解析:(1)![]() ,
,
![]() ,令
,令![]() ,得
,得![]() . 1分
. 1分
列表:
x |
|
|
|
|
| 0 | + |
| ↘ | 极小值 | ↗ |
所以![]() 的极小值为
的极小值为![]() ,无极大值. 4分
,无极大值. 4分
(2)当![]() 时,假设存在实数
时,假设存在实数![]() 满足条件,则
满足条件,则![]() 在
在![]() 上恒成立. 5分
上恒成立. 5分
1)当![]() 时,
时, 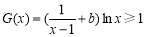 可化为
可化为![]() ,
,
令![]() ,问题转化为:
,问题转化为:![]() 对任意
对任意![]() 恒成立;(*)
恒成立;(*)
则![]() ,
,![]() ,
,![]() .
.
令![]() ,则
,则![]() .
.
①![]() 时,因为
时,因为![]() ,
,
故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递减,
时单调递减,![]() ,
,
即![]() ,从而函数
,从而函数![]() 在
在![]() 时单调递增,故
时单调递增,故![]() ,所以(*)
,所以(*)
成立,满足题意; 7分
②当![]() 时,
时, ,
,
因为![]() ,所以
,所以![]() ,记
,记![]() ,则当
,则当![]() 时,
时,![]() ,
,
故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,
即![]() ,从而函数
,从而函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(*)不成立;
,此时(*)不成立;
所以当![]() ,
,![]() 恒成立时,
恒成立时,![]() ; 9分
; 9分
2)当![]() 时,
时,![]() 可化为
可化为![]() ,
,
令![]() ,问题转化为:
,问题转化为:![]() 对任意的
对任意的![]() 恒成立;(**)
恒成立;(**)
则![]() ,
,![]() ,
,![]() .
.
令![]() ,则
,则![]() .
.
①![]() 时,
时,![]() ,
,
故![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,
即![]() ,从而函数
,从而函数![]() 在
在![]() 时单调递增,所以
时单调递增,所以![]() ,此时(**)成立;11分
,此时(**)成立;11分
②当![]() 时,
时,
ⅰ)若![]() ,必有
,必有![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,从而函数
,从而函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(**)不成立; 13分
,此时(**)不成立; 13分
ⅱ)若![]() ,则
,则![]() ,所以当
,所以当![]() 时,
时,
 ,
,
故函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,即
,即![]() ,所以函数
,所以函数![]() 在
在![]() 时单调递减,所以
时单调递减,所以![]() ,此时(**)不成立;
,此时(**)不成立;
所以当![]() ,
,![]() 恒成立时,
恒成立时,![]() ; 15分
; 15分
综上所述,当![]() ,
,![]() 恒成立时,
恒成立时, ![]() ,从而实数
,从而实数![]() 的取值集合为
的取值集合为![]() . 16分
. 16分


科目:高中数学 来源: 题型:
【题目】(本题满分16分)
设函数![]() .
.
(1)若![]() =1时,函数
=1时,函数![]() 取最小值,求实数
取最小值,求实数![]() 的值;
的值;
(2)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意正整数
,证明对任意正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班25人的成绩记为AI(I=1,2,…,25)由右边的程序运行后,输出n=10.据此解答如下问题: 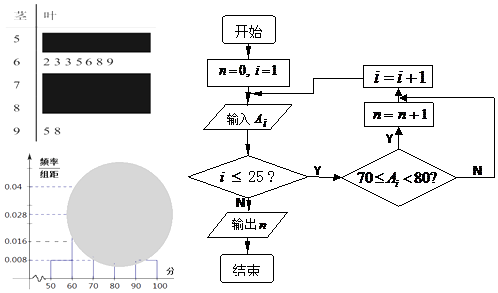
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x﹣cos4x的最小正周期是π;
② ![]() =tanα;
=tanα;
③函数y=sinx+cosx的图象均关于点( ![]() ,0)成中心对称;
,0)成中心对称;
④把函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象.
其中正确命题的编号是 . (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,令
时,令![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a、b、c是常数,则“a>0且b2﹣4ac<0”是“对任意x∈R,有ax2+bx+c>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先把正弦函数y=sinx图象上所有的点向左平移 ![]() 个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的
个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的 ![]() 倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的
倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),则所得函数图象的解析式是( )
倍(纵坐标不变),则所得函数图象的解析式是( )
A.y=2sin( ![]() x+
x+ ![]() )
)
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )
)
C.y=2sin( ![]() x﹣
x﹣ ![]() )
)
D.y= ![]() sin(2x+
sin(2x+ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com