
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
【答案】
(1)解:∵a=1,b=﹣2时,f(x)=x2﹣x﹣3,
f(x)=xx2﹣2x﹣3=0x=﹣1,x=3
∴函数f(x)的不动点为﹣1和3
(2)解:即f(x)=ax2+(b+1)x+b﹣1=x有两个不等实根,
转化为ax2+bx+b﹣1=0有两个不等实根,须有判别式大于0恒成立
即b2﹣4a(b﹣1)>0△=(﹣4a)2﹣4×4a<00<a<1,
∴a的取值范围为0<a<1
(3)解:设A(x1,x1),B(x2,x2),则x1+x2=﹣ ![]() ,
,
A,B的中点M的坐标为 ( ![]() ,
, ![]() ),即M(﹣
),即M(﹣ ![]() ,﹣
,﹣ ![]() )
)
∵A、B两点关于直线y=kx+ ![]() 对称,
对称,
又因为A,B在直线y=x上,
∴k=﹣1,A,B的中点M在直线y=kx+ ![]() 上.
上.
∴﹣ ![]() =
= ![]() b=﹣
b=﹣ ![]() =﹣
=﹣ ![]() 利用基本不等式可得
利用基本不等式可得
当且仅当a= ![]() 时,b的最小值为﹣
时,b的最小值为﹣ ![]()
【解析】(1)转化为直接解方程x2﹣x﹣3=x即可.(2)转化为ax2+bx+b﹣1=0有两个不等实根,转化为b2﹣4a(b﹣1)>0恒成立,再利用二次函数大于0恒成立须满足的条件来求解即可.(3)利用两点关于直线对称的两个结论,一是中点在已知直线上,二是两点连线和已知直线垂直.找到a,b之间的关系式,整理后在利用基本不等式求解可得.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数![]() 的图象是一条抛物线,对称轴方程为
的图象是一条抛物线,对称轴方程为![]() 顶点坐标是
顶点坐标是![]() ;当
;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】记等比数列{an}前n项和为Sn , 已知a1+a3=30,3S1 , 2S2 , S3成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=3,bn+1﹣3bn=3an , 求数列{bn}的前n项和Bn;
(3)删除数列{an}中的第3项,第6项,第9项,…,第3n项,余下的项按原来的顺序组成一个新数列,记为{cn},{cn}的前n项和为Tn , 若对任意n∈N* , 都有 ![]() >a,试求实数a的最大值.
>a,试求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图(b)所示. 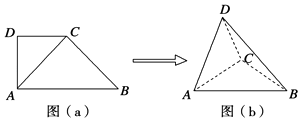
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:对m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立;命题q:不等式x2+ax+2<0有解.若p是真命题,q是假命题,求a的取值范围.
恒成立;命题q:不等式x2+ax+2<0有解.若p是真命题,q是假命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,令
时,令![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 .
(注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …,xn的平均数)
为x1 , x2 , …,xn的平均数)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x0 , x0+ ![]() 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣ ![]() )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点
(1)求 ![]() 的值;
的值;
(2)若对 ![]() ,都有|f(x)﹣m|≤1,求实数m的取值范围.
,都有|f(x)﹣m|≤1,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com