
【题目】如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图(b)所示. 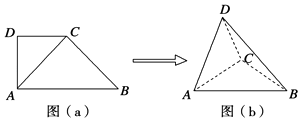
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
【答案】
(1)证明:在图中,可得AC=BC=4 ![]() ,从而AC2+BC2=AB2,
,从而AC2+BC2=AB2,
故AC⊥BC,又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC平面ABC,
∴BC⊥平面ACD
(2)解:由(1)可知,BC为三棱锥B﹣ACD的高,BC=4 ![]() ,S△ACD=8,
,S△ACD=8,
∴VB﹣ACD= ![]() S△ACDBC=
S△ACDBC= ![]() ×8×4
×8×4 ![]() =
= ![]() ,
,
由等体积性可知,几何体D﹣ABC的体积为 ![]()
【解析】(1)证明AC⊥BC,利用平面与平面垂直的性质定理,证明BC⊥平面ACD.(2)由(1)可知,BC为三棱锥B﹣ACD的高,求出BC,S△ACD , 即可求解VB﹣ACD , 由等体积性可知,求解几何体D﹣ABC的体积.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() ,
, ![]() ,
, ![]() 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 与
与 ![]() 所成角的大小;
所成角的大小;
(2)记f(x)=| ![]() |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个.从中任取一球,得到红球的概率是 ![]() ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是 ![]() ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是 ![]() .
.
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是“红球或绿球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( ) 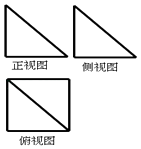
A.![]()
B.4 ![]() π
π
C.12π
D.![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班25人的成绩记为AI(I=1,2,…,25)由右边的程序运行后,输出n=10.据此解答如下问题: 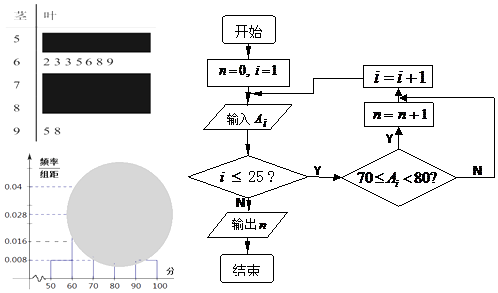
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥S﹣ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)如图,我市有一个健身公园,由一个直径为2km的半圆和一个以![]() 为斜边的等腰直角三角形
为斜边的等腰直角三角形![]() 构成,其中
构成,其中![]() 为
为![]() 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道![]() ,按实际需要,四边形
,按实际需要,四边形![]() 的两个顶点
的两个顶点![]() 分别在线段
分别在线段![]() 上,另外两个顶点
上,另外两个顶点![]() 在半圆上,
在半圆上, ![]() ,且
,且![]() 间的距离为1km.设四边形
间的距离为1km.设四边形![]() 的周长为
的周长为![]() km.
km.

(1)若![]() 分别为
分别为![]() 的中点,求
的中点,求![]() 长;
长;
(2)求周长![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com