
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
设事件A,B,已知P(A)= ,P(B)=
,P(B)= ,P(A∪B)=
,P(A∪B)=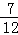 ,则A,B之间的关系一定为( )
,则A,B之间的关系一定为( )
A.互斥事件 B.两个任意事件 C.非互斥事件 D.对立事件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习文科数学试卷(解析版) 题型:解答题
已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆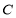 过点
过点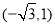 且与抛物线
且与抛物线 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆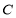 方程;
方程;
(2)直线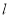 过椭圆
过椭圆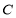 的右焦点
的右焦点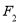 且斜率为
且斜率为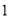 与椭圆
与椭圆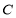 交于
交于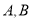 两点,求弦
两点,求弦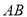 的长;
的长;
(3)以第(2)题中的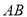 为边作一个等边三角形
为边作一个等边三角形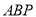 ,求点
,求点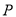 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习理科数学试卷(解析版) 题型:解答题
请仔细阅读以下材料:
已知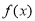 是定义在
是定义在 上的单调递增函数.
上的单调递增函数.
求证:命题“设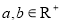 ,若
,若 ,则
,则 ”是真命题.
”是真命题.
证明 :因为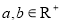 ,由
,由 得
得 .
.
又因为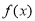 是定义在
是定义在 上的单调递增函数,
上的单调递增函数,
于是有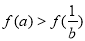 . ①
. ①
同理有 . ②
. ②
由① + ②得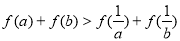 .
.
故,命题“设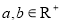 ,若
,若 ,则
,则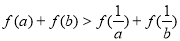 ”是真命题.
”是真命题.
请针对以上阅读材料中的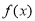 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设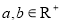 ,若
,若 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于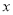 的不等式
的不等式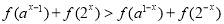 (其中
(其中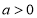 ).
).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次定时练习数学试卷(解析版) 题型:选择题
定义在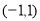 上的函数
上的函数 ;当
;当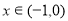 时,
时,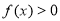 ,若
,若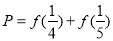 ,
,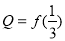 ,
,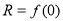 ,则P,Q,R的大小关系为( )
,则P,Q,R的大小关系为( )
A. Q>P>R B. P>Q>R C. R>Q>P D. R>P>Q
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高一上学期10月月考数学试卷(解析版) 题型:填空题
函数f(x)在R上为奇函数,且当x>0时,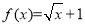 ,则x<0时的解析式为f(x)=________.
,则x<0时的解析式为f(x)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com