
已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆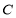 过点
过点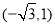 且与抛物线
且与抛物线 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆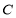 方程;
方程;
(2)直线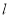 过椭圆
过椭圆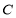 的右焦点
的右焦点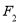 且斜率为
且斜率为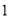 与椭圆
与椭圆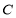 交于
交于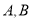 两点,求弦
两点,求弦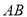 的长;
的长;
(3)以第(2)题中的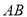 为边作一个等边三角形
为边作一个等边三角形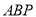 ,求点
,求点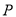 的坐标.
的坐标.
(1) ;(2)
;(2) ;(3)
;(3)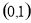 或
或 .
.
【解析】
试题分析:(1)设椭圆的方程,若焦点明确,设椭圆的标准方程,结合条件用待定系数法求出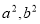 的值,若不明确,需分焦点在
的值,若不明确,需分焦点在 轴和
轴和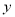 轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
轴上两种情况讨论;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式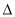 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)涉及弦长的问题时,应熟练地利用根与系数的关系,设而不求计算弦长;直线与圆锥曲线相交所得中的弦问题,就解析几何的内容之一,一般有以下三种类型:①求中点弦所在的直线方程;②求弦中点的轨迹方程问题;③弦长为定值时,弦中点的坐标问题,其解法有代点相减法、设而不求法、参数法、待定系数法及中心对称变换法.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)涉及弦长的问题时,应熟练地利用根与系数的关系,设而不求计算弦长;直线与圆锥曲线相交所得中的弦问题,就解析几何的内容之一,一般有以下三种类型:①求中点弦所在的直线方程;②求弦中点的轨迹方程问题;③弦长为定值时,弦中点的坐标问题,其解法有代点相减法、设而不求法、参数法、待定系数法及中心对称变换法.
试题解析:(1)由题意得 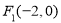
 2分
2分
又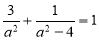 ,
,
得, ,解得
,解得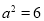 或
或 (舍去), 2分
(舍去), 2分
则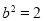 , 1分
, 1分
故椭圆方程为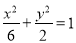 . 1分
. 1分
(2)直线 的方程为
的方程为 . 1分
. 1分
联立方程组
消去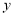 并整理得
并整理得 . 3分
. 3分
设 ,
,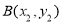 .
.
故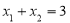 ,
, . 1分
. 1分
则
 2分
2分
(3)设 的中点为
的中点为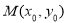 .
.
可得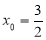 , 1分
, 1分
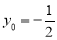 . 1分
. 1分
线段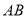 的中垂线
的中垂线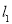 斜率为
斜率为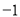 , 所以
, 所以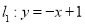
设 1分
1分
所以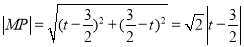 . 1分
. 1分
当△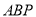 为正三角形时,
为正三角形时,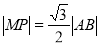 ,
,
可得 , 解得
, 解得 或
或 . 2分
. 2分
即 ,或
,或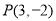 . 1分
. 1分
考点:1、求椭圆的标准方程;2、直线与圆相交求弦长;3、直线与椭圆的综合问题.


科目:高中数学 来源:2014-2015学年甘肃省高一上学期期末考试数学试卷(解析版) 题型:解答题
已知四棱锥P-ABCD,底面ABCD是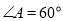 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.

(Ⅰ)证明:DN//平面PMB;
(Ⅱ)证明:平面PMB 平面PAD;
平面PAD;
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率0.03,出现丙级品的概率0.01,则对产品抽查一次抽得正品的概率是( )
A.0.09 B.0.98 C.0.97 D.0.96
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁四个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件
B.不可能事件
C.互斥事件但不是对立事件
D.以上答案都不对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
(2014•郑州一模)将一枚质地均匀的硬币连掷4次,出现“至少两次正面向上”的概率为( )
A. B.
B. C.
C.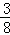 D.
D.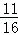
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习文科数学试卷(解析版) 题型:填空题
关于曲线 ,给出下列四个结论:
,给出下列四个结论:
①曲线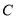 是椭圆;
是椭圆;
②关于坐标原点中心对称;
③关于直线 轴对称;
轴对称;
④所围成封闭图形面积小于8.
则其中正确结论的序号是 .(注:把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南德宏州芒市高一上学期期末考试数学试卷(解析版) 题型:选择题
下列给出函数 与
与 的各组函数中,表示相等函数的是 ( )
的各组函数中,表示相等函数的是 ( )
A.
B.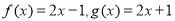
C.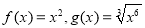
D.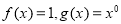
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com