
分析 (1)对f(x)求导得到g(x),对g(x)求导,由导函数为正得到单调增区间,导函数为负,得到单调减区间.
(2)由f(x)的导函数,对a 进行分类讨论.当a≥$\frac{1}{e}$时和当0<a<$\frac{1}{e}$时两种情形.
解答 解:(1)g(x)=f′(x)=lnx+$\frac{a}{x}$,
∴g(x)的定义域为(0,+∞),
g′(x)=$\frac{x-a}{{x}^{2}}$,
①当a≤0时,g′(x)>0恒成立,g(x)的单调增区间是(0,+∞).
②当a>0时,g′(x)>0时得x>a,即g(x)的单调增区间是(a,+∞),单调减区间是(0,a).
综上所述:当a≤0时,g(x)的单调增区间是(0,+∞).
当a>0时,g(x)的单调增区间是(a,+∞),单调减区间是(0,a).
(2)a>0时,由(1)知,f′(x)的递减区间为(0,a),递增区间为(a,+∞),
∴f′(x)最小值为f′(a)=lna+1,
①当a≥$\frac{1}{e}$时,有 f′(a)≥0恒成立,
∴f(x)为(0,+∞)上的增函数,
又 f($\frac{1}{e}$)=($\frac{1}{e}$+a)ln$\frac{1}{e}$-e+a=-$\frac{2}{e}$<0,
∴f(e)=(e+a)lne-e+a=2a>0,
∴f($\frac{1}{e}$)f(e)<0,
∴?x0∈($\frac{1}{e}$,e),使得f(x0)=0,
∵f(x)在(0,+∞)上的增函数,
∴x=x0为(0,+∞)的唯一的零点,
②当0<a<$\frac{1}{e}$时,f′(x)min=f′(a)=lna+1<0,
由条件提供的命题:“?a>0,?0<x<a,使得a+xlnx>0”为真命题.
即知?a>0,?0<x<a,使得f′(x)=lnx+$\frac{a}{x}$=$\frac{a+xlnx}{x}$>0,
∵f′(x)在区间(0,a)上为减函数,
∴x∈(0,x1),f′(x)>0,x∈(x1,a),f′(x)<0,
又∵f′(e)=lne+$\frac{a}{e}$=$\frac{a}{e}$+1>0,
∴f′(a)f′(e)<0,
∴?x2∈(a,e),使得f′(x2)=0,
∵f′(x)在区间(a,+∞)上为增函数,
∴x∈(a,x2),f′(x)<0,x∈(x2,+∞),f′(x)>0,
∴f(x)的递增区间为(0,x1)和(x2,+∞),递减区间为(x1,a)和(a,x2),
∵0<x1<a<$\frac{1}{e}$,∴lnx1<-1,
∴f(x1)=(x1+a)lnx1-x1+a<-(x1+a)-x1+a=-2x1<0,
∵f(x)在(x1,x2)上为递减函数,
∴f(x2)<0,
∴x∈(0,x2),f(x)<0恒成立,
∵x→+∞,f(x)→+∞,
∴在区间(x2,+∞)上,函数f(x)有且只有一个零点.
综上,a>0时,函数f(x)有且只有一个零点.
点评 本题考查函数求导,求导后对a进行讨论,确定单调区间,及确定函数零点问题,同样需要对a进行分类讨论,较难.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{7}{3}$ | C. | $\frac{7}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,-1) | C. | (-∞,-3) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
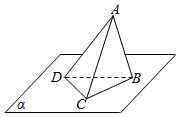 如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.
如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com