
分析 (1)由椭圆的离心率及过点P($\sqrt{6}$,1),列出方程组求出a,b,由此能求出椭圆E的方程.
(2)假设存在这样的圆,设该圆的切线为y=kx+m,与椭圆联立,得(1+2k2)x2+4kmx+2m2-8=0,由此利用根的判别式、韦达定理、圆的性质,结合已知条件能求出|AB|的取值范围.
解答 解:(1)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,且过点P($\sqrt{6}$,1),
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{6}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=8,b2=4,
∴椭圆E的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
(2)假设存在这样的圆,设该圆的切线为y=kx+m,
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(1+2k2)x2+4kmx+2m2-8=0
△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,
${x}_{1}+{x}_{2}=-\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}$,
y1y2=( kx1+m ) ( kx2+m )=k2x1x2+km ( x1+x2)+m2=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$,
∵$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,∴x1x2+y1y2=0,
∴$\frac{2{m}^{2}-8}{1+2{k}^{2}}+\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$=0,∴3m2-8k2-8=0,∴k2=$\frac{3{m}^{2}-8}{8}$≥0
又 8k2-m2+4>0,∴$\left\{\begin{array}{l}{{m}^{2}>2}\\{3{m}^{2}≥8}\end{array}\right.$,∴m2≥$\frac{8}{3}$,∴m≥$\frac{2\sqrt{6}}{3}$或m≤-$\frac{2\sqrt{6}}{3}$,
又y=kx+m与圆心在原点的圆相切,
∴r=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,即${r}^{2}=\frac{{m}^{2}}{1+{k}^{2}}$=$\frac{{m}^{2}}{1+\frac{3{m}^{2}-8}{8}}$=$\frac{8}{3}$,r=$\frac{2\sqrt{6}}{3}$,
∴所求圆:x2+y2=$\frac{8}{3}$,
当切线斜率不存在时,切线为x=±$\frac{2\sqrt{6}}{3}$,
与椭圆$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1交于($\frac{2\sqrt{6}}{3}$,$±\frac{2\sqrt{6}}{3}$)或(-$\frac{2\sqrt{6}}{3}$,$±\frac{2\sqrt{6}}{3}$),
满足OA⊥OB,
综上:存在这样的圆x2+y2=$\frac{8}{3}$满足条件,
∵|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{\frac{32(4{k}^{4}+5{k}^{2}+1)}{3(4{k}^{4}+4{k}^{2}+1)}}$=$\sqrt{\frac{32}{3}(1+\frac{{k}^{2}}{4{k}^{4}+4{k}^{2}+1})}$,
当k≠0时,|AB|=$\sqrt{\frac{32}{3}(1+\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4})}$,
∴$\frac{4\sqrt{6}}{3}<$|AB|$≤2\sqrt{3}$(当k=±$\frac{\sqrt{2}}{2}$时取等号)
当k=0时,|AB|=$\frac{4\sqrt{6}}{3}$,
当k不存时,|AB|=$\frac{4\sqrt{6}}{3}$,
∴|AB|∈[$\frac{4\sqrt{6}}{3}$,2$\sqrt{3}$].
点评 本题考查椭圆方程的求法,考查满足条件的圆是否存在的判断及弦长的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、圆的性质、椭圆性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
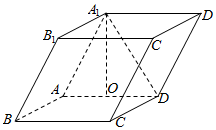 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{{\sqrt{7}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com