
分析 根据等腰三角形“三线合一”,得到|MP|=|F2P|,从而|PF1|+|PF2|=|MF1|,结合椭圆的定义可得|MF1|=2a,运用中位线定理,即可得到动点P的轨迹对应的图形.
解答 解:椭圆x2+2y2=8,即为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,
可得a=2$\sqrt{2}$,
$\overrightarrow{AP}•\overrightarrow{{F_2}P}$=0,可得$\overrightarrow{AP}$⊥$\overrightarrow{{F}_{2}P}$,
延长F1A和F2P交于M,连接OP,
可得|MP|=|F2P|,即有|PF1|+|PF2|=|AM|+|AF2|=|MF1|,
根据椭圆的定义,可得|PF1|+|PF2|=4$\sqrt{2}$,
∴|MF1|=4$\sqrt{2}$,
由中位线定理可得|OP|=$\frac{1}{2}$|MF1|=2$\sqrt{2}$,
因此,点P的轨迹是以点O为圆心,半径为2$\sqrt{2}$的圆x2+y2=8.
故答案为:x2+y2=8.
点评 本题给出椭圆上动点A,求点P的轨迹方程,着重考查了椭圆的定义和简单几何性质,以及等腰三角形“三线合一”等知识,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,-1) | C. | (-∞,-3) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.| A. | 3,1,6;60 | B. | 3,1,6;70 | C. | 3,2,5;60 | D. | 3,2,5;70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
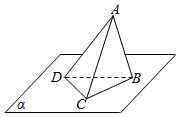 如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.
如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
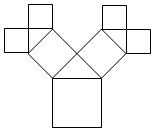 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com