
分析 (1)由向量数量积的坐标运算结合辅助角公式化简,再由周期求得ω,则函数解析式可求,由此求得f(x)的最大值及取得最大值时x的集合;
(2)由x得范围求得相位的范围,进一步求得f(x)在区间$[{0,\frac{2π}{3}}]$上的取值范围.
解答 解:(1)f(x)=$\overrightarrow a•\overrightarrow b$=$si{n}^{2}ωx+\sqrt{3}sinωxsin(ωx+\frac{π}{2})$
=$\frac{1-cos2ωx}{2}+\frac{\sqrt{3}}{2}sin2ωx$=$\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1}{2}cos2ωx+\frac{1}{2}$
=$sin(2ωx-\frac{π}{6})+\frac{1}{2}$.
∵函数f(x)的最小正周期为π,且ω>0,
∴$\frac{2π}{ω}$=π,解得ω=1,
∴f(x)=sin(2x$-\frac{π}{6}$)$+\frac{1}{2}$.
∴f(x)的最大值为$\frac{3}{2}$,此时$2x-\frac{π}{6}=\frac{π}{2}+2kπ,k∈Z$,即$x=\frac{π}{3}+kπ,k∈Z$.
∴使f(x)取得最大值时x的集合为{x|$x=\frac{π}{3}+kπ,k∈Z$};
(2)由(1)得f(x)=sin(2x$-\frac{π}{6}$)$+\frac{1}{2}$.
∵0$≤x≤\frac{2π}{3}$,
∴$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{7π}{6}$,
∴$-\frac{1}{2}≤sin(2x-\frac{π}{6})≤1$,
因此0≤$sin(2x-\frac{π}{6})+\frac{1}{2}≤\frac{3}{2}$,
即f(x)的取值范围为[0,$\frac{3}{2}$].
点评 本题考查三角函数中的恒等变换应用,考查了三角函数的图象和性质,训练了平面向量数量积的坐标运算,是中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
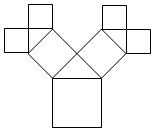 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
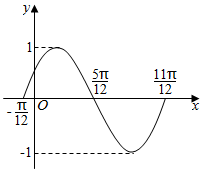
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com