分析:(法一)
(I)由正方形的性质可得AC⊥DB,而A
1C在平面ABCD内的斜线,由三垂线的逆定理可得A
1C⊥BD①,又A
1C在平面BB
1C
1C内的射影
B
1C⊥BE,同理可得BEA
1C⊥BE②由①②根据直线与平面垂直的判定定理可证
(II)由(I)可得EF⊥平面A
1B
1C,考虑连接DF,根据三垂线定理可得∠EDF即为直线ED与平面A
1B
1C所成的角,在直角三角形EDF中,求解∠EDF即可.
(法二)如图以A为原点,建立空间直角坐标系A-xyz,
(I)要证A
1C⊥平面EBD?
⊥, ⊥?
•=0 ,•=0,利用向量的数量积的坐标表示可证
(II)分别求解平面A
1B
1C的一个法向量为
,DE与平面A
1B
1C所成角转化为
与所成的角,代入公式
cosθ=可求
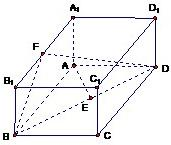
解答: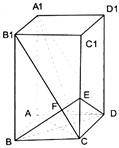
法一:(I)证明:连接AC,由底面ABCD为正方形,得AC⊥DB.
∵AC是A
1C在平面ABCD内的射影,∴A
1C⊥BD
又∵A
1B
1⊥平面BB
1C
1C,且A
1C在平面BB
1C
1C内的射影B
1C⊥BE,
∴A
1C⊥BE,又BE∩BD=B∴A
1C⊥平面EBD
(Ⅱ)解:连接DF,A
1D∵EF⊥B
1C,EF⊥A
1C
∴EF⊥平面A
1B
1C∴∠EDF即为直线ED与平面A
1B
1C所成的角
由条件AB=BC=1,BB
1=2
可知
B1C=,BF=,B1F=,CF=EF==,EC==∴
ED==∴
sinEDF==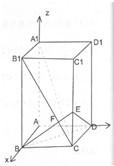
解法二:(I)证明:如图以A为原点,建立空间直角坐标系A-xyz,
则∵
•=1×0+1×1+(-2)×=0,•=1×1+1×0+(-2)×=0∴
⊥,⊥,
即A
1C⊥BE,A
1C⊥DE∵BE∩DE=E∴A
1C⊥平面EBD;
(Ⅱ)解:设平面A
1B
1C的一个法向量为
=(x,y,z)
则
∴令z=1,得m=(0,2,1),又
=(-1,0,-)设
与
所成角为θ,则
cosθ==-.从而把直线
∴直线ED与平面A
1B
1C所成角的正弦值为
.
点评:本题主要考查了空间直线与平面的位置关系:垂直关系的判定定理的运用,直线与平面所成角的求解,在解决此类问题时,采用空间向量的方法,可以很容易寻求解题思路,但要注意直线与平面所成的角的范围.

 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C. 法一:(I)证明:连接AC,由底面ABCD为正方形,得AC⊥DB.
法一:(I)证明:连接AC,由底面ABCD为正方形,得AC⊥DB. 解法二:(I)证明:如图以A为原点,建立空间直角坐标系A-xyz,
解法二:(I)证明:如图以A为原点,建立空间直角坐标系A-xyz,

 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F