
分析 (1)只要证明:($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0即可.
(2)2$\overrightarrow{a}$+$\overrightarrow{b}$=(2cosa+cosp,2sina+sinp.可得|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{(2cosa+cosp)^{2}+(2sina+sinp)^{2}}$=$\sqrt{5+4cos(a-p)}$,利用cos(a-p)≤1即可得出.
解答 (1)证明:$\overrightarrow{a}$+$\overrightarrow{b}$=(cosa+cosp,sina+sinp).$\overrightarrow{a}$-$\overrightarrow{b}$=(cosa-cosp,sina-sinp).
($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=(cos2a-cos2p)+(sin2a-sin2p)=1-1=0,
因此$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直.
(2)解:2$\overrightarrow{a}$+$\overrightarrow{b}$=(2cosa+cosp,2sina+sinp.
|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{(2cosa+cosp)^{2}+(2sina+sinp)^{2}}$
=$\sqrt{5+4cos(a-p)}$≤$\sqrt{9}$=3.
当且仅当cos(a-p)=1时取等号.
∴|2$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值为3.
点评 本题考查了向量垂直与数量积的关系、三角函数的值域,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
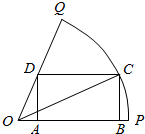 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com