
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
���� ����Ƶ�ʷֲ�ֱ��ͼ���������жϣ�
����ƽ��������������λ���ĸ����жϣ�
����Ƶ�ʷֲ�ֱ��ͼ���ص��жϣ�
���ɷ��ʽ��֪��һ�����ݶ����ϻ��ȥͬһ����������䣻
��һ�����Իع鷽��$\stackrel{��}{y}$=3-5x������x����1����λʱ��yƽ����С5����λ��֪�ݴ���
��� �⣺����Ƶ�ʷֲ�ֱ��ͼ�У�С���ε������ʾƵ�ʣ��ʢٴ���
��ƽ��������������λ���Ӳ�ͬ�ĽǶ�������һ�����ݵļ������ƣ��ʢ���ȷ��
�۴�Ƶ�ʷֲ�ֱ��ͼ�ò���ԭʼ���������ݣ������ݱ�ʾ��ֱ��ͼ��ԭ�еľ���������Ϣ�ͱ�Ĩ���ˣ��ʢ���ȷ��
�ܸ��ݷ��ʽ����֪��һ�������е�ÿ�����ݶ����ϻ��ȥͬһ����������㲻�䣬�ʢ���ȷ��
������һ�����Իع鷽��$\stackrel{��}{y}$=3-5x������x����1����λʱ��yƽ����С5����λ���ʢݴ���
���ȷ�Ľ�����2����
��ѡ��B��
���� ���⿼�����������ж���Ӧ�ã��������Իع鷽�̡������Լ��顢����ı仯�ص㣬��һ������֪ʶ��Ƚ϶����Ŀ���ؼ����������ǻ����⣮


 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1+2i | B�� | 1-2i | C�� | 1+2i | D�� | -2-3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 13 | C�� | 1��13 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
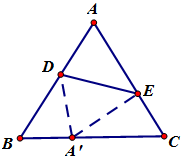 �ڡ�ABC�У�a��b��c�ֱ�Ϊ�ڽ�A��B��C���Եıߣ�������$\frac{tanA}{tanB}=\frac{2c-b}{b}$��
�ڡ�ABC�У�a��b��c�ֱ�Ϊ�ڽ�A��B��C���Եıߣ�������$\frac{tanA}{tanB}=\frac{2c-b}{b}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.5 | B�� | -0.5 | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com