
【题目】已知直线![]() 与抛物线
与抛物线![]() 相切,且与
相切,且与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() .若动点
.若动点![]() 与两定点
与两定点![]() 所构成三角形的周长为6.
所构成三角形的周长为6.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ) 设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,当
两点,当![]() ,且
,且![]() 位于直线
位于直线![]() 的两侧时,证明:
的两侧时,证明: ![]() .
.
【答案】(Ⅰ) ![]() (
(![]() );(Ⅱ)见解析.
);(Ⅱ)见解析.
【解析】试题分析:(Ⅰ先由判别式为零可得![]() 的值,再根据三角形周长可得
的值,再根据三角形周长可得![]() 进而由椭圆定义可得方程;(Ⅱ)设直线
进而由椭圆定义可得方程;(Ⅱ)设直线![]() 方程
方程![]() ,联立
,联立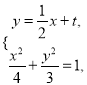 得
得![]() ,根据直线斜率公式及韦达定理利用分析法证明
,根据直线斜率公式及韦达定理利用分析法证明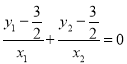 即可.
即可.
试题解析:(Ⅰ) 因为直线![]() 与抛物线
与抛物线![]() 相切,所以方程
相切,所以方程![]() 有等根,
有等根,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
又因为动点![]() 与定点
与定点![]() 所构成的三角形周长为6,且
所构成的三角形周长为6,且![]() ,
,
所以![]()
根据椭圆的定义,动点![]() 在以
在以![]() 为焦点的椭圆上,且不在
为焦点的椭圆上,且不在![]() 轴上,
轴上,
所以![]() ,得
,得![]() ,则
,则![]() ,
,
即曲线![]() 的方程为
的方程为![]() (
(![]() ).
).
(Ⅱ)设直线![]() 方程
方程![]()
![]() ,联立
,联立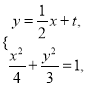 得
得![]() ,
,
△=-3![]() +12>0,所以
+12>0,所以![]() , 此时直线
, 此时直线![]() 与曲线
与曲线![]() 有两个交点
有两个交点![]() ,
, ![]() ,
,
设![]()
![]() ,
, ![]()
![]() ,则
,则![]() ,
, ![]()
∵![]() ,不妨取
,不妨取![]() ,
,
要证明![]() 恒成立,即证明
恒成立,即证明![]() ,
,
即证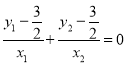 ,也就是要证
,也就是要证![]()
即证![]() 由韦达定理所得结论可得此式子显然成立,
由韦达定理所得结论可得此式子显然成立,
所以![]() 成立.
成立.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数![]() 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ),
),![]() ,
,
(Ⅰ) 试求曲线![]() 在点
在点![]() 处的切线l与曲线
处的切线l与曲线![]() 的公共点个数;(Ⅱ) 若函数
的公共点个数;(Ⅱ) 若函数![]() 有两个极值点,求实数a的取值范围.
有两个极值点,求实数a的取值范围.
(附:当![]() ,x趋近于0时,
,x趋近于0时, ![]() 趋向于
趋向于![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]()
![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
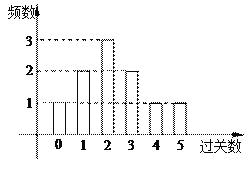
(Ⅰ)估计小明在1次游戏中所得奖品数的期望值;
(Ⅱ)估计小明在3 次游戏中至少过两关的平均次数;
(Ⅲ)估计小明在3 次游戏中所得奖品超过30件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
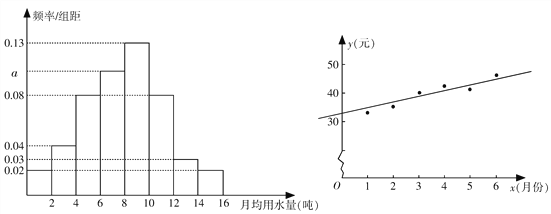
(图1) (图2)
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() . 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
. 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分10分)
已知椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,离心率
,离心率![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .求证:以
.求证:以![]() 为直径的圆恒过一定点
为直径的圆恒过一定点![]() .并求出点
.并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
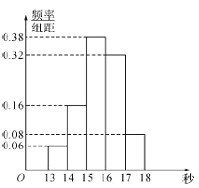
(1)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均值(精确到![]() );
);
(2)若从第一、五组中随机取出两个成绩,列举所有选取方法,并求这两个成绩的差的绝对值大于1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com