练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，四边形与均为菱形， ，且.

    (l)求证：

    (2)求证：

    (3)设，求四面体的体积

    【答案】（1）见解析;（2）见解析;（3） .

    【解析】试题分析：（1）证线面垂直根据题意可先证，（2）线面平行证明则只需证线线平行也可通过面面平行得到结论因为四边形与均为菱形，所以又，所以平面 （3）求体积可根据等体积法求解

    试题解析：（1）证明：设AC与BD相交于点O，连结FO.

    因为四边形ABCD为菱形，所以，

    又FA=FC，且O为AC中点.所以.

    因为，

    所以.

    （2）证明：因为四边形与均为菱形，

    所以

    又，

    所以平面

    又

    所以.

    （3）解：因为四边形BDEF为菱形，且，

    所以为等边三角形．

    因为为中点，所以

    由（1）知 ，故 .

    又

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】矩形的两条对角线相交于点， 边所在的直线的方程为，点在边所在的直线上．　

    （1）求边所在直线的方程；

    （2）求矩形外接圆的方程；

    （3）过点的直线被矩形的外接圆截得的弦长为，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C经过点，且圆心在直线上，又直线与圆C交于P,Q两点.

    （1）求圆C的方程；

    （2）若，求实数的值；

    (3)过点作直线，且交圆C于M,N两点，求四边形的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线与抛物线相切，且与轴的交点为，点.若动点与两定点所构成三角形的周长为6．

    (Ⅰ) 求动点的轨迹的方程；

    (Ⅱ) 设斜率为的直线交曲线于两点，当，且位于直线的两侧时，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， ， ，斜率为的直线过点，且和以为圆相切.

    （1）求圆的方程；

    （2）在圆上是否存在点，使得，若存在，求出所有的点的坐标；若不存在说明理由；

    （3）若不过的直线与圆交于， 两点，且满足， ， 的斜率依次为等比数列，求直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正方体ABCD﹣A1B1C1D1的棱长为8cm，M，N，P分别是AB，A1D1 ， BB1的中点．
    （1）画出过M，N，P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线；
    （2）设过M，N，P三点的平面与B1C1交于Q，求PQ的长．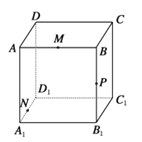

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直三棱柱ABC﹣A1B1C1中，若∠BAC=90°，AB=AC=AA1 ， 则异面直线BA1与AC1所成的角等于（　　）

    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为减少空气污染，某市鼓励居民用电（减少燃气或燃煤），采用分段计费的方法计算电费．每月用电不超过100度时，按每度0.57元计算，每月用电量超过100度时，其中的100度仍按原标准收费，超过的部分每度按0.5元计算．
    （1）设月用电x度时，应交电费y元，写出y关于x的函数关系式；
    （2）小明家第一季度缴纳电费情况如下：问小明家第一季度共用电多少度？

    月份

    一月

    二月

    三月

    合计

    交费金额

    76元

    63元

    45.6元

    184.6元

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若不等式（1－a）x2－4x＋6>0的解集是{x|－3<x<1}．

    （1）解不等式2x2＋（2－a）x－a>0；

    （2）b为何值时，ax2＋bx＋3≥0的解集为R.

    查看答案和解析>>

    同步练习册答案